Advertisements
Advertisements
Question
Solve the following problem.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
Solution
Given: h = 300 km = 0.3 × 106 m, M = 5.98 × 1024 kg, R = 6400 km = 6.4 × 106 m, G = 6.67 × 10-11 Nm2/kg2
To find: Acceleration due to gravity at height (gh)
Formula: `"g"_"h" = "GM"/("R + h")^2`
Calculation:
From formula,
`"g"_"h" = (6.67 xx 10^-11 xx 5.98 xx 10^24)/([(6.4 xx 10^6) + (0.3 xx 10^6)]^2)`
`= (6.67 xx 5.98 xx 10^13)/((6.7)^2 xx 10^12)`
= antilog{log(6.67) + log(5.98) - 2log(6.7)} × 10
= antilog{0.8241 + 0.7767 - 2(0.8261)} × 10
= antilog{1.6008 - 1.6522} × 10
= antilog{`bar1`.9486} × 10
= 0.8884 × 10
= 8.884 m/s2
Acceleration due to gravity at 300 km will be 8.884 m/s2.
APPEARS IN
RELATED QUESTIONS
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
What happens to the force between two objects, if the distance between the objects is doubled and tripled?
Calculate the force of gravitation between the earth and the Sun, given that the mass of the earth = 6 × 1024 kg and of the Sun = 2 × 1030 kg. The average distance between the two is 1.5 × 1011 m.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
State Kepler’s law which is represented by the relation r3 ∝ T2.
State the universal law of gravitation. Name the scientist who gave this law.
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.
Suppose the gravitational potential due to a small system is k/r2 at a distance r from it. What will be the gravitational field? Can you think of any such system? What happens if there were negative masses?
Let V and E be the gravitational potential and gravitational field at a distance r from the centre of a uniform spherical shell. Consider the following two statements :
(A) The plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
A person sitting in a chair in a satellite feels weightless because
Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre of the triangle.
Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
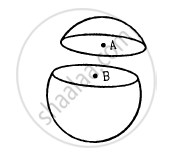
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the final velocity of the ball on reaching the ground .
Who stated the law of gravitation?
How will the force of gravitation between two objects change if the distance between them is:
Made four times
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
The force of attraction between any two material objects is called __________.
Is the law of gravitation applicable in case of the sun and the moon?
A ball is thrown up with a speed of 4.9 ms-1.
Calculate the maximum height it would gain before it begins to fall.
What does a force do in the following case?
You twist a piece of rubber.
What does a force do in the following case?
You catch a kicked ball.
Name and state the action and reaction in the following case:
A person walking on the ground.
Is there a gravitational attraction between you and the book? Explain.
The gravitational force between two bodies is directly proportional to the product of the masses of those bodies and is _______ of the distance between them.
As observed from earth, the sun appears to move in an approximate circular orbit. For the motion of another planet like mercury as observed from earth, this would ______.
Complete the chart below.
| F(N) | M1(kg) | M2(kg) | D(m) |
| (a) | 50 | 84 | 02 |
| 16 × 109 | 1.63 × 1022 | (b) | 34 |
Four identical particles of equal masses 1 kg made to move along the circumference of a circle of radius 1 m under the action of their own mutual gravitational attraction. The speed of each particle will be ______.
If three equal masses m are placed at the three vertices of an equilateral triangle of side 1/m then what force acts on a particle of mass 2m placed at the centroid?
