Advertisements
Advertisements
Question
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
Advertisements
Solution 1
Mass of the Sun, Ms = 2 × 1030 kg
Mass of the Earth, Me = 6 × 10 24 kg
Orbital radius, r = 1.5 × 1011 m
Mass of the rocket = m
Let x be the distance from the centre of the Earth where the gravitational force acting on satellite P becomes zero.
From Newton’s law of gravitation, we can equate gravitational forces acting on satellite P under the influence of the Sun and the Earth as:
`(GmM_s)/(r-x)^2 = GmM_e/x^2`
((r-x)/x)^2 = `M_s/M_e`
`(r-x)/r = ((2xx10^(30))/(60xx10^(24)))^(1/2) = 577.35`
`1.5 xx 10^(11)-x=577.35x`
`x = (1.5xx10^11)/578.35` = `2.59 xx 10^8` m
Solution 2
Mass of Sun, M = 2 x 1030 kg; Mass of Earth, m = 6 x 1024 kg Distance between Sim and Earth, r = 1.5 x 1011 m
Let at the point P, the gravitational force on the rocket due to Earth = gravitional force on the rocket due to sun
Let x = distance of the point { from the Earth
Then `(Gm)/x^2 = (GM)/(r-x)^2`
`=>(r-x)^2/x^2 = M/m = (2xx10^(30))/(6xx10)^24 = 10^6/3`
or `(r-x)/x = 10^3/sqrt3 => r/x = 10^3/sqrt3 + 1 =~ 10^3/sqrt3`
or `x = (sqrt3r)/10^3 = (1.732xx1.5xx10^11)/10^3 = 2.6 xx 10^8` m
RELATED QUESTIONS
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
Can you think of two particles which do not exert gravitational force on each other?
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
A body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in an orbit of radius R and is W2 when it goes in an orbit of radius 2 −R.
Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
(a) is zero in any small part of the orbit
(b) is zero in some parts of the orbit
(c) is zero in one complete revolution
(d) is zero in no part of the motion.
Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1+ R2)/2 from the centre?
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
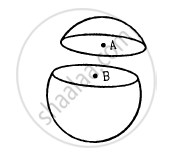
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the total time of journey of the ball .
Multiple Choice Question. Select the correct option.
The mass of earth is 6 × 1024 kg and radius of earth is 6.4 × 106 m. The magnitude of force between the mass of 1 kg and the earth is:
Who stated the law of gravitation?
How will the force of gravitation between two objects change if the distance between them is:
Infinite
At what height above the earth's surface would the value of acceleration due to gravity be half of what it is on the surface? Take the radius of earth to be R.
What does a force do in the following case?
You apply brakes to a running car.
You can change the direction in which an object is moving by___________.
An apple falls towards the earth due to its gravitational force. The apple also attracts the earth with the same force. Why do we not see the earth rising towards the apple? Explain.
Answer the following question.
What are the dimensions of the universal gravitational constant?
If three equal masses m are placed at the three vertices of an equilateral triangle of side 1/m then what force acts on a particle of mass 2m placed at the centroid?
The acceleration of the Moon towards the Earth is approximately:
