Advertisements
Advertisements
Question
How will you ‘weigh the sun’, that is estimate its mass? The mean orbital radius of the earth around the sun is 1.5 × 108 km.
Solution 1
Orbital radius of the Earth around the Sun, r = 1.5 × 1011 m
Time taken by the Earth to complete one revolution around the Sun,
T = 1 year = 365.25 days
= 365.25 × 24 × 60 × 60 s
Universal gravitational constant, G = 6.67 × 10–11 Nm2 kg–2
Thus, mass of the Sun can be calculated using the relation,
`M = (4pi^2r^3)/(GT^2)`
= `(4xx(3.14)^2 xx (1.5xx10^11)^3)/(6.67xx10^(11)xx(365.25xx24xx60xx60))^2`
=`(133.24xx10)/(6.64xx10^(4)) = 2.0xx10^(30)` kg
Hence, the mass of the Sun is 2 × 1030 kg.
Solution 2
The mean orbital radius of the Earth around the Sun
R = 1.5 x 108 km = 1.5 x 1011 m
Time period, T = 365.25 x 24 x 60 x 60 s
Let the mass of the Sun be M and that of Earth be m.
According to law of gravitation
`F= G(Mm)/RA^2` ...(i)
Centripetal force
`F = (mv^2)/R = m.R.omega^2` ...(ii)
`(GMm)/R^2 = m.R.omega^2`
=`(mR.4pi^2)/T^2`
`:. M = (4pi^2R^3)/(G.T^2)` [∵ `omega = (2pi)/T`]
= `(4xx(3.14)^2xx(1.5xx10^11)^3)/(6.67xx10^(-11)xx(365.25 xx 24 xx 60xx60)^2)`
= `2.009 xx 10^(30) kg = 2.0 xx 10^(30) kg`
APPEARS IN
RELATED QUESTIONS
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
Choose the correct alternative:
Acceleration due to gravity increases/decreases with increasing altitude.
Choose the correct alternative:
Acceleration due to gravity is independent of mass of the earth/mass of the body.
State two applications of universal law of gravitation.
Can you think of two particles which do not exert gravitational force on each other?
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
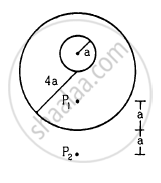
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a (In the following figure). The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at the points P1 and P2 shown in the figure.
Solve the following problem.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
Molecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
