Advertisements
Advertisements
Question
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
Advertisements
Solution
Let d be distance of the particle from the centre of the Earth.
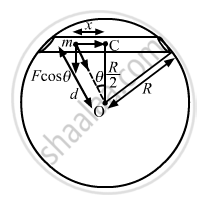
\[\text { Now }, d^2 = x^2 + \left( \frac{R^2}{4} \right) = \frac{4 x^2 + R^2}{4}\]
\[ \Rightarrow d = \left( \frac{1}{2} \right)\sqrt{4 x^2 + R^2}\]
Let M be the mass of the Earth and M' be the mass of the sphere of radius d.
Then we have :
\[M = \left( \frac{4}{3} \right)\pi R^3 \rho\]
\[ M^1 = \left( \frac{4}{3} \right)\pi d^3 \rho\]
\[ \therefore \frac{M^1}{M} = \frac{d^3}{R^3}\]
Gravitational force on the particle of mass m is given by
\[F = \frac{G M^1 m}{d^2}\]
\[ \Rightarrow F = \frac{G d^3 Mm}{R^3 d^2}\]
\[ \Rightarrow F = \frac{GMm}{R^3}d\]
∴ Normal force exerted by the wall, FN = F cos θ
\[= \frac{GMmd}{R^3} \times \frac{R}{2d} = \frac{GMm}{2 R^2}\]
APPEARS IN
RELATED QUESTIONS
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
Choose the correct answer from among the given ones:
For the problem 8.10, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow (i) d, (ii) e, (iii) f, (iv) g.
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object, as measured by a spring balance on the earth's surface, more at midnight as compared to its weight at noon?
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
Define one Newton. How much maximum acceleration can it produce in a mass of 1 kg?
How will the force of gravitation between two objects change if the distance between them is:
Infinite
Is the law of gravitation applicable in case of the sun and the moon?
Why don't you feel the force of attraction between your friend sitting close to you and yourself?
Where will you weigh more: at the moon's surface or at the earth's surface?
Two equal and opposite forces acting at the same point on a stationary body. Will the body move? Give reason to explain your answer.
State the universal law of gravitation and derive its mathematical expression.
Law of gravitation gives the gravitational force between
How is the gravitational force between two point masses affected when they are dipped in water keeping the separation between them the same?
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
