Advertisements
Advertisements
प्रश्न
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
उत्तर
Let d be distance of the particle from the centre of the Earth.
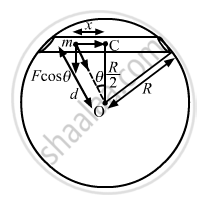
\[\text { Now }, d^2 = x^2 + \left( \frac{R^2}{4} \right) = \frac{4 x^2 + R^2}{4}\]
\[ \Rightarrow d = \left( \frac{1}{2} \right)\sqrt{4 x^2 + R^2}\]
Let M be the mass of the Earth and M' be the mass of the sphere of radius d.
Then we have :
\[M = \left( \frac{4}{3} \right)\pi R^3 \rho\]
\[ M^1 = \left( \frac{4}{3} \right)\pi d^3 \rho\]
\[ \therefore \frac{M^1}{M} = \frac{d^3}{R^3}\]
Gravitational force on the particle of mass m is given by
\[F = \frac{G M^1 m}{d^2}\]
\[ \Rightarrow F = \frac{G d^3 Mm}{R^3 d^2}\]
\[ \Rightarrow F = \frac{GMm}{R^3}d\]
∴ Normal force exerted by the wall, FN = F cos θ
\[= \frac{GMmd}{R^3} \times \frac{R}{2d} = \frac{GMm}{2 R^2}\]
APPEARS IN
संबंधित प्रश्न
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.
The law of gravitation gives the gravitational force between :
State whether the gravitational force between two masses is attractive or repulsive ?
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
A ball is thrown up with a speed of 4.9 ms-1.
Calculate the maximum height it would gain before it begins to fall.
At what height above the earth's surface would the value of acceleration due to gravity be half of what it is on the surface? Take the radius of earth to be R.
What does a force do in the following case?
You pull the skin of your arm
What does a force do in the following case?
You twist a piece of rubber.
What is the difference between gravity and gravitation?
Explain why:
The atmosphere does not escape.
The distance-time values for an object moving along straight line are given below:
| Time (s) | Distance (m) |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
Different points in earth are at slightly different distances from the sun and hence experience different forces due to gravitation. For a rigid body, we know that if various forces act at various points in it, the resultant motion is as if a net force acts on the c.m. (centre of mass) causing translation and a net torque at the c.m. causing rotation around an axis through the c.m. For the earth-sun system (approximating the earth as a uniform density sphere).
If the law of gravitation, instead of being inverse-square law, becomes an inverse-cube law- ______.
- planets will not have elliptic orbits.
- circular orbits of planets is not possible.
- projectile motion of a stone thrown by hand on the surface of the earth will be approximately parabolic.
- there will be no gravitational force inside a spherical shell of uniform density.
Write the answer of the question with reference to laws of gravitation.
Write the value of the universal gravitational constant.
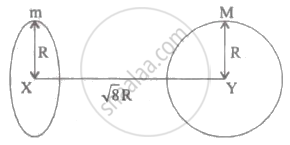
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.