Advertisements
Advertisements
प्रश्न
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
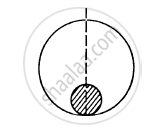
उत्तर
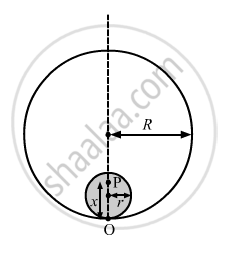
(a) Consider that the particle is placed at a distance x from O.
Here, r < x < 2r
Let us consider a thin solid sphere of radius (x \[-\] r).
Mass of the sphere,
\[dm = \frac{m}{\left( \frac{4}{3} \right)\pi r^3} \times \frac{4}{3}\pi(x - r )^3 = \frac{m(x - r )^3}{r^3}\]
Then the gravitational force on the particle due to the solid sphere is given by
\[F = \frac{Gm' dm}{(x - r )^2}\]
\[ = \frac{G\frac{m(x - r )^3}{r^3}m'}{(x - r )^2} = \frac{Gmm'(x - r)}{r^3}\]
Force on the particle due to the shell will be zero because gravitational field intensity inside a shell is zero.
(b) If 2r < x < 2R,
Force on the body due to the shell will again be zero as particle is still inside the shell.
then F is only due to the solid sphere.
\[\therefore F = \frac{Gmm'}{\left( x - r \right)^2}\]
(c) If x > 2R, then the gravitational force is due to both the sphere and the shell.
Now, we have :
Gravitational force due to shell,
\[F = \frac{GMm'}{\left( x - R \right)^2}\]
Gravitational force due to the sphere \[= \frac{Gmm'}{\left( x - r \right)^2}\]
As both the forces are acting along the same line joining the particle with the centre of the sphere and shell so both the forces can be added directly without worrying about their vector nature.
∴ Resultant force \[= \frac{Gmm'}{\left( x - r \right)^2} + \frac{GMm'}{\left( x - R \right)^2}\]
APPEARS IN
संबंधित प्रश्न
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
How does the force of gravitation between two objects change when the distance between them is reduced to half?
What happens to the force between two objects, if the mass of one object is doubled?
What happens to the force between two objects, if the distance between the objects is doubled and tripled?
Answer the following:
You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object, as measured by a spring balance on the earth's surface, more at midnight as compared to its weight at noon?
A person sitting in a chair in a satellite feels weightless because
Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1+ R2)/2 from the centre?
The gravitational field in a region is given by \[E = \left( 2 \overrightarrow{i} + 3 \overrightarrow{j} \right) N {kg}^{- 1}\] . Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
[Hint : If a line y = mx + c makes angle θ with the X-axis, m = tan θ.]
The law of gravitation gives the gravitational force between :
How will the force of gravitation between two objects change if the distance between them is:
Almost zero
The force of attraction between any two material objects is called __________.
Is the law of gravitation applicable in case of the sun and the moon?
What is meant by the equation :
`g= Gxxm/r^2`
where the symbols have their usual meanings.
What does a force do in the following case?
You catch a kicked ball.
Explain why:
The atmosphere does not escape.
Is there a gravitational attraction between you and the book? Explain.
The value of universal gravitational constant (G) in the SI unit is ______.
For the weight of body of mass 5 kg to be zero on equator of the earth, angular velocity of the earth must be (The radius of earth = 6400 km, acceleration due to gravity = 10 m/s2).
The force of gravitation between two bodies of mass 1 kg each separated by a distance of 1 m in vacuum is ____________.
