Advertisements
Advertisements
प्रश्न
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
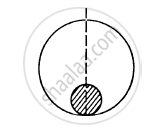
उत्तर
(a) Consider that the particle is placed at a distance x from O.
Here, r < x < 2r
Let us consider a thin solid sphere of radius (x \[-\] r).
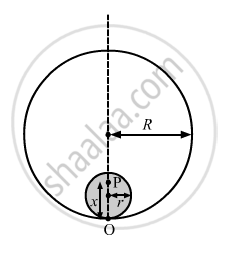
Mass of the sphere,
\[dm = \frac{m}{\left( \frac{4}{3} \right)\pi r^3} \times \frac{4}{3}\pi(x - r )^3 = \frac{m(x - r )^3}{r^3}\]
Then the gravitational force on the particle due to the solid sphere is given by
\[F = \frac{Gm' dm}{(x - r )^2}\]
\[ = \frac{G\frac{m(x - r )^3}{r^3}m'}{(x - r )^2} = \frac{Gmm'(x - r)}{r^3}\]
Force on the particle due to the shell will be zero because gravitational field intensity inside a shell is zero.
(b) If 2r < x < 2R,
Force on the body due to the shell will again be zero as particle is still inside the shell.
then F is only due to the solid sphere.
\[\therefore F = \frac{Gmm'}{\left( x - r \right)^2}\]
(c) If x > 2R, then the gravitational force is due to both the sphere and the shell.
Now, we have :
Gravitational force due to shell,
\[F = \frac{GMm'}{\left( x - R \right)^2}\]
Gravitational force due to the sphere \[= \frac{Gmm'}{\left( x - r \right)^2}\]
As both the forces are acting along the same line joining the particle with the centre of the sphere and shell so both the forces can be added directly without worrying about their vector nature.
∴ Resultant force \[= \frac{Gmm'}{\left( x - r \right)^2} + \frac{GMm'}{\left( x - R \right)^2}\]
APPEARS IN
संबंधित प्रश्न
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
Can you think of two particles which do not exert gravitational force on each other?
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements:
(A) the plot of V against r is discontinuous.
(B) The plot of E against r is discontinuous.
The law of gravitation gives the gravitational force between :
Write an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r.
Who stated the law of gravitation?
How will the force of gravitation between two objects change if the distance between them is:
Doubled
Where will you weigh more: at the centre of the earth or at the surface of the earth?
What does a force do in the following case?
You pull the skin of your arm
Name and state the action and reaction in the following case:
Hammering a nail.
An apple falls towards the earth due to its gravitational force. The apple also attracts the earth with the same force. Why do we not see the earth rising towards the apple? Explain.
What do you mean by a gravitational constant?
Solve the following problem.
Calculate the acceleration due to gravity at a height of 300 km from the surface of the Earth. (M = 5.98 × 1024 kg, R = 6400 km).
The value of universal gravitational constant (G) in the SI unit is ______.
Three uniform spheres, each having mass m and radius r, are kept in such a way that each touches the other two. The magnitude of the gravitational force on any sphere due to the other two is
We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
The gravitational force between a hollow spherical shell (of radius R and uniform density) and a point mass is F. Show the nature of F vs r graph where r is the distance of the point from the centre of the hollow spherical shell of uniform density.
Answer the following questions in reference to the figure below:
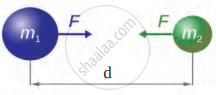
- Which relation is shown in the figure?
- What will happen if the mass of one of the objects is doubled?
