Advertisements
Advertisements
प्रश्न
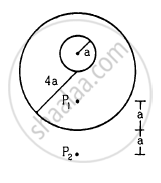
A uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and radius 4a (In the following figure). The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at the points P1 and P2 shown in the figure.
उत्तर
At point P1, the gravitational field due to the sphere and the shell is given by
F \[= \frac{GM}{\left( 3a + a \right)^2} + 0 = \frac{GM}{16 a^2}\]
At point P2, the gravitational field due to the sphere and the shell is given by
\[F = \frac{GM}{\left( a + 4a + a \right)^2} + \frac{GM}{\left( 4a + a \right)^2}\]
\[ \Rightarrow F = \frac{GM}{36 a^2} + \frac{GM}{25 a^2}\]
\[ \Rightarrow F = \frac{GM}{a^2}\left( \frac{1}{36} + \frac{1}{25} \right)\]
\[ \Rightarrow F = \frac{GM}{a^2}\left( \frac{25 + 36}{900} \right)\]
\[ \Rightarrow F = \left( \frac{61}{900} \right)\frac{GM}{a^2}\]
APPEARS IN
संबंधित प्रश्न
Write the formula to find the magnitude of the gravitational force between the earth and an object on the surface of the earth.
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Answer the following:
You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be? Can one of the three particles be?
Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre of the triangle.
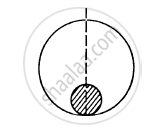
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
The gravitational field in a region is given by \[E = \left( 2 \overrightarrow{i} + 3 \overrightarrow{j} \right) N {kg}^{- 1}\] . Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
[Hint : If a line y = mx + c makes angle θ with the X-axis, m = tan θ.]
Who stated the law of gravitation?
How will the force of gravitation between two objects change if the distance between them is:
Halved
How will the force of gravitation between two objects change if the distance between them is:
Doubled
A force can produce ________, In an object at rest. It can __________ an object and change its __________ of motion.
What does a force do in the following case?
You twist a piece of rubber.
What does a force do in the following case?
You catch a kicked ball.
What is the difference between gravity and gravitation?
Gravity is another kind of ________. It exerts all through the ________. The Sun's gravity keeps the ___________ in their orbits. Gravity can only be felt with very large ________.
Explain the difference between g and G.
Solve the following problem.
Find the gravitational force between the Sun and the Earth.
Given Mass of the Sun = 1.99 × 1030 kg
Mass of the Earth = 5.98 × 1024 kg
The average distance between the Earth and the Sun = 1.5 × 1011 m.
Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure). At subsequent times before any collision takes place ______.

Two particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle with respect to its centre of mass is ______.
