Advertisements
Advertisements
प्रश्न
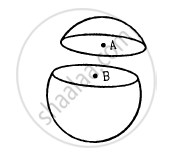
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in the following figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational field at A due to the first part is equal in magnitude to the gravitational field at B due to the second part.
उत्तर
We know that in a thin spherical shell of uniform density, the gravitational field at its internal point is zero. So, at points A and B, the gravitational fields are equal and opposite and, thus, cancel each other. So the net field is zero.
Hence, EA = EB
APPEARS IN
संबंधित प्रश्न
The earth and the moon are attracted to each other by gravitational force. Does the earth attract the moon with a force that is greater or smaller or the same as the force with which the moon attracts the earth? Why?
Which of the Kepler’s laws of planetary motion led Newton to establish the inverse-square rule for gravitational force between two bodies ?
State the universal law of gravitation. Name the scientist who gave this law.
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.
The weight of an object is more at the poles than at the equator. Is it beneficial to purchase goods at equator and sell them at the pole? Does it matter whether a spring balance is used or an equal-beam balance is used?
A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m s −1 as it reaches A. The work done by the person on the mass is −3 J. The potential at A is
Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
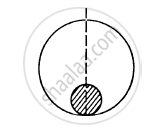
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
A ball is thrown vertically upwards. It goes to a height 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the total time of journey of the ball .
Where will you weigh more: at the centre of the earth or at the surface of the earth?
Explain the difference between g and G.
The value of universal gravitational constant (G) in the SI unit is ______.
The force of gravitation between two bodies of mass 1 kg each separated by a distance of 1 m in vacuum is ____________.
Choose the wrong option.
Molecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
Write the answer of the question with reference to laws of gravitation.
Write the value of the universal gravitational constant.
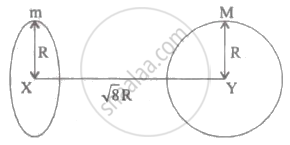
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If `sqrt8` R is the distance between the centres of a ring (of mass 'm')and a sphere (mass 'M') where both have equal radius 'R'.
Newton's universal law of gravitation applies to ______.
