Advertisements
Advertisements
Question
Answer the following:
An astronaut inside a small space ship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?
Solution 1
If the size of the space station is large enough, then the astronaut will detect the change in Earth’s gravity (g).
Solution 2
Yes. If the size of the spaceship is extremely large, then the gravitational effect of the spaceship may become measurable. The variation in g can also be detected.
APPEARS IN
RELATED QUESTIONS
Calculate the force of gravitation between the earth and the Sun, given that the mass of the earth = 6 × 1024 kg and of the Sun = 2 × 1030 kg. The average distance between the two is 1.5 × 1011 m.
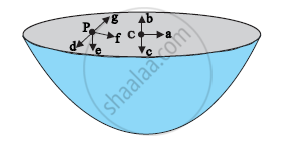
The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig 8.12) (i) a, (ii) b, (iii) c, (iv) 0.
A rocket is fired from the earth towards the sun. At what distance from the earth’s centre is the gravitational force on the rocket zero? Mass of the sun = 2 ×1030 kg, mass of the earth = 6 × 1024 kg. Neglect the effect of other planets etc. (orbital radius = 1.5 × 1011 m).
Inside a uniform spherical shell
(a) the gravitational potential is zero
(b) the gravitational field is zero
(c) the gravitational potential is same everywhere
(d) the gravitational field is same everywhere
Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.
A ball is thrown up with a speed of 4.9 ms-1.
Calculate the maximum height it would gain before it begins to fall.
Explain why:
The atmosphere does not escape.
Answer the following question.
What are the dimensions of the universal gravitational constant?
Particles of masses 2M, m and M are respectively at points A, B and C with AB = ½ (BC). m is much-much smaller than M and at time t = 0, they are all at rest (Figure). At subsequent times before any collision takes place ______.

We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
