Question

Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.

Answer 1

Consider a small mass element of length dx at a distance x from the centre of the rod.
Mass of the mass element, dm = (M/L) × dx

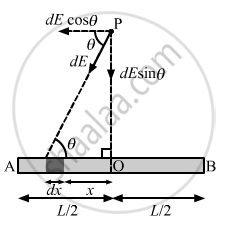
Gravitational field due to this element at point P is given by \[dE = \frac{G\left( dm \right) \times 1}{\left( d^2 + x^2 \right)}\]

The components of the gravitational field due to the symmetrical mass element along the length of the rod cancel each other.

Now, resultant gravitational field = 2dE sin θ

\[= 2 \times \frac{G\left( dm \right)}{\left( d^2 + x^2 \right)} \times \frac{d}{\sqrt{\left( d^2 + x^2 \right)}}\]

\[ = \frac{2 \times GM \times d dx}{L\left( d^2 + x^2 \right) \left\{ \left( \sqrt{d^2 + x^2} \right) \right\}}\]

Total gravitational field due to the rod at point P is given by \[E = \int_0^{L/2} \frac{2Gmd \ dx}{L \left( d^2 + x^2 \right)^{3/2}}\]

On integrating the above equation, we get :

 

\[E = \frac{2Gm}{d\sqrt{L^2 + 4 d^2}}\]