Advertisements
Advertisements
प्रश्न
Suppose the gravitational potential due to a small system is k/r2 at a distance r from it. What will be the gravitational field? Can you think of any such system? What happens if there were negative masses?
उत्तर
The gravitational potential due to the system is given as \[V = \frac{k}{r^2}\]
Gravitational field due to the system :
\[E = - \frac{dV}{dr}\]
\[ \Rightarrow E = - \frac{d}{dr}\left( \frac{k}{r^2} \right) = - \left( - \frac{2k}{r^3} \right)\]
\[ \Rightarrow E = \frac{2k}{r^3}\]
We can see that for this system , \[E \propto \frac{1}{r^3}\]
This type of system is not possible because \[F_g\] is always proportional to inverse of square of distance(experimental fact).
If there were negative masses, then this type of system is possible.
This system is a dipole of two masses, i.e., two masses, one positive and the other negative, separated by a small distance.
In this case, the gradational field due to the dipole is proportional to \[\frac{1}{r^3}\]
APPEARS IN
संबंधित प्रश्न
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
What is the magnitude of the gravitational force between the earth and a 1 kg object on its surface? (Mass of the earth is 6 × 1024 kg and radius of the earth is 6.4 × 106 m).
Calculate the force of gravitation between the earth and the Sun, given that the mass of the earth = 6 × 1024 kg and of the Sun = 2 × 1030 kg. The average distance between the two is 1.5 × 1011 m.
If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the Moon’s pull is greater than the tidal effect of Sun. Why?
Choose the correct alternative:
Acceleration due to gravity increases/decreases with increasing depth. (assume the earth to be a sphere of uniform density).
Can we apply Newton’s third law to the gravitational force ? Explain your answer.
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.
Can you think of two particles which do not exert gravitational force on each other?
A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the following figure . A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if (a) r < x < 2r, (b) 2r < x < 2R and (c) x > 2R.
The gravitational field in a region is given by \[E = \left( 2 \overrightarrow{i} + 3 \overrightarrow{j} \right) N {kg}^{- 1}\] . Show that no work is done by the gravitational field when a particle is moved on the line 3y + 2x = 5.
[Hint : If a line y = mx + c makes angle θ with the X-axis, m = tan θ.]
The mass of moon is about 0.012 times that of earth and its diameter is about 0.25 times that of earth. The value of G on the moon will be:
Name and state the action and reaction in the following case:
A person walking on the ground.
Give the applications of universal law gravitation.
Answer the following questions in reference to the figure below:
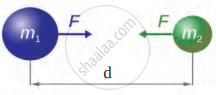
- Which relation is shown in the figure?
- What will happen if the mass of one of the objects is doubled?
Newton's universal law of gravitation applies to ______.
