Advertisements
Advertisements
Question
A park is of the shape of a circle of diameter 7 m. It is surrounded by a path of width of 0·7 m. Find the expenditure of cementing the path, if its cost is Rs 110 per sq. m ?
Solution
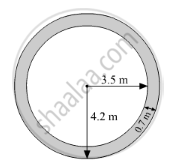
Diameter of the circular park = 7 m
∴ Radius of the circular park, r =\[\frac{7}{2}\] = 3.5 m
Width of the path = 0.7 m
∴ Radius of the park including the path, R = 3.5 + 0.7 = 4.2 m
Area of the path
\[= \pi R^2 - \pi r^2 \]
\[ = \pi\left( R^2 - r^2 \right)\]
\[= \frac{22}{7}\left( 4 . 2^2 - 3 . 5^2 \right)\]
\[ = \frac{22}{7} \times \left( 4 . 2 - 3 . 5 \right) \times \left( 4 . 2 + 3 . 5 \right)\]
\[ = \frac{22}{7} \times 0 . 7 \times 7 . 7\]
\[ = 16 . 94 m^2\]
Rate of cementing the path = Rs 110/m2 (Given)
∴ Total cost of cementing the path
= 16.94 × 110
= Rs 1863.40
Thus, the expenditure of cementing the path is Rs 1863.40.
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 5 cm. Draw two tangents to this circle so that the angle between the tangents is 45°.
Draw a circle circumscribing a regular hexagon with side 5 cm.
Construct a triangle ABC in which base BC = 5.5 cm, AB = 6 cm and ∠ABC = 120°.
- Construct a circle circumscribing the triangle ABC.
- Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle 30° with a line passing through the centre.
Draw a circle with centre O and radius 2.5 cm. Take a point P at a distance of 6 cm from the centre. Using ruler and compasses only construct the tangents to the circle from the point P.
Using ruler and compasses only, draw tangents to a circle of radius 3 cm from a point 5 cm from the centre. What is the length of each of them ?
Draw two circles with radii 2.5 cm and 4 cm and with their centres 7 cm apart.
Draw a direct common tangent and a transverse common tangent. Calculate the length of the direct common tangent.
Take a point O on the plane at the paper. With O as center draw a circle of radius 3 cm. Take a point P on this circle and draw a tangent at P.
Using ruler and compass construct a triangle ABC in which AB = 6 cm, ∠BAC = 120° and AC = 5 cm. Construct a circle passing through A, B and C. Measure and write down the radius of the circle.
