Advertisements
Advertisements
Question
A point object is placed at a distance of 15 cm from a convex lens. The image is formed on the other side at a distance of 30 cm from the lens. When a concave lens is placed in contact with the convex lens, the image shifts away further by 30 cm. Calculate the focal lengths of the two lenses.
Solution
Given,
Distance between point object and convex lens, u = 15 cm
Distance between the image of the point object and convex lens, v = 30 cm
Let fc be the focal length of the convex lens.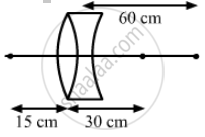
Then, using lens formula, we have:
\[\frac{1}{v} - \frac{1}{u} = \frac{1}{f_c}\]
\[ \Rightarrow \frac{1}{f_c} = \frac{1}{30} - \frac{1}{( - 15)}\]
\[ \Rightarrow \frac{1}{f_c} = \frac{1}{30} + \frac{1}{15} = \frac{3}{30}\]
\[ \Rightarrow f_c = 10 \text{ cm }\]
Now, as per the question, the concave lens is placed in contact with the convex lens. So the image is shifted by a distance of 30 cm.
Again, let vf be the final image distance from concave lens, then:
\[v_f\] = + (30 + 30) = + 60 cm
Object distance from the concave lens, v = 30 cm
If fd is the focal length of concave lens then
Using lens formula, we have:
\[\frac{1}{v_f} - \frac{1}{v} = \frac{1}{f_d}\]
\[ \Rightarrow \frac{1}{f_d} = \frac{1}{60} - \frac{1}{30}\]
\[ \Rightarrow \frac{1}{f_d} = \frac{30 - 60}{60 \times 30} = \frac{- 30}{60 \times 30}\]
\[ \Rightarrow f_d = - 60 \text{ cm }\]
Hence, the focal length (fc ) of convex lens is 10 cm and that of the concave lens (fd ) is 60 cm.
APPEARS IN
RELATED QUESTIONS
The equation of refraction at a spherical surface is \[\frac{\mu_2}{\nu} - \frac{\mu_1}{\mu} = \frac{\mu_2 - \mu_1}{R}\]
Taking \[R = \infty\] show that this equation leads to the equation
\[\frac{\text{ Real depth }}{\text{ Apparent depth }} = \frac{\mu_2}{\mu_1}\]
for refraction at a plane surface.
A convex lens has a focal length of 10 cm. Find the location and nature of the image if a point object is placed on the principal axis at a distance of (a) 9.8 cm, (b) 10.2 cm from the lens.
An extended object is placed at a distance of 5.0 cm from a convex lens of focal length 8.0 cm. (a) Draw the ray diagram (to the scale) to locate the image and from this, measure the distance of the image from the lens. (b) Find the position of the image from the lens formula and see how close the drawing is to the correct result.
A converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart. If a pin of length 2.0 cm is placed 30 cm from the lens farther away from the mirror, where will the final image form and what will be the size of the final image?
A 5 mm high pin is placed at a distance of 15 cm from a convex lens of focal length 10 cm. A second lens of focal length 5 cm is placed 40 cm from the first lens and 55 cm from the pin. Find (a) the position of the final image, (b) its nature and (c) its size.
Two convex lenses, each of focal length 10 cm, are placed at a separation of 15 cm with their principal axes coinciding. (a) Show that a light beam coming parallel to the principal axis diverges as it comes out of the lens system. (b) Find the location of the virtual image formed by the lens system of an object placed far away. (c) Find the focal length of the equivalent lens. (Note that the sign of the focal length is positive although the lens system actually diverges a parallel beam incident on it.)
A ball is kept at a height h above the surface of a heavy transparent sphere made of a material of refractive index μ. The radius of the sphere is R. At t = 0, the ball is dropped to fall normally on the sphere. Find the speed of the image formed as a function of time for \[t < \sqrt{\frac{2h}{g}}\] . Consider only the image by a single refraction.
Use the above relation to obtain the condition on the position of the object and the radius of curvature in terms of n1and n2 when the real image is formed.
Define the term 'focal length of a mirror'.
According to new Cartesian sign conventions, all the distances are measured from the ______.
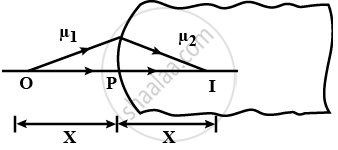
A spherical surface of radius R separates two medium of refractive indices µ1 and µ2, as shown in figure. Where should an object be placed in the medium 1 so that a real image is formed in medium 2 at the same distance?
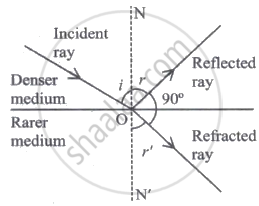
A ray of light from a denser medium strikes a rarer medium at an angle of incidence i as shown in the figure. Refracted and reflected rays make an angle of 90° with each other. The angle of reflection and refraction are r and r'. The critical angle is ______.
Define the critical angle for a given pair of media and total internal reflection. Obtain the relation between the critical angle and refractive index of the medium.
A point object in the air is placed symmetrically at a distance of 60 cm in front of a concave spherical surface with a refractive index of 1.5. If the radius of curvature of the surface is 20 cm, find the position of the image formed.
Assertion: If critical angle of glass-air pair `("μg" = 3/2)` is θ1 and that of water-air pair `("μw" = 4/3)` is θ2, then the critical angle for the water-glass pair will lie between θ1 and θ2.
Reason: A medium is optically denser if its refractive index is greater.
