Advertisements
Advertisements
Question
Use the above relation to obtain the condition on the position of the object and the radius of curvature in terms of n1and n2 when the real image is formed.
Solution

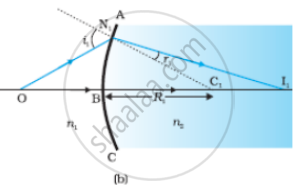
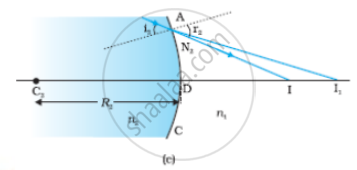
(a) The position of the object, and the image formed by a double convex lens,
(b) Refraction at the first spherical surface and (c) Refraction at the second spherical surface.
Figure (a) shows the geometry of image formation by a double convex lens. The image formation can be seen in terms of two steps: (i) The first refracting surface forms the image I1 of the object O [Fig. (b)]. The image I1 acts as a virtual object for the second surface that forms the image at I [Fig. (c)].
Applying Equation `"n"_2/"v"-"n"_1/"u" = ("n"_2-"n"_1)/"R"` to the first interface ABC,
We get
`"n"_1/"OB" + "n"_2/"BI"_1 = ("n"_2-"n"_1)/"BC"_1` ......(1)
A similar procedure applied to the second interface ADC gives,
`"n"_2/"DI"_1 +"n"_1/"DI" = ("n"_2-"n"_1)/"DC"_1` ......(2)
For a thin lens, BI1= DI1. Adding
Eqs. (1) and (2), we get
`"n"_1/"OB" + "n"_1/"DI" = ("n"_2 - "n"_1)(1/"BC"_1+1/"DC"_2)`.....(3)
Suppose the object is at infinity, i.e., `"OB" -> ∞ and "DI" = f, Eq.(3) "gives"`
`"n"_1/f = ("n"_2-"n"_2)(1/"BC"_1 + 1/"DC"_2) ......(4)`
The point where image of an object placed at infinity is formed is called the focus F, of the lens and the distance f gives its focal length.
By the sign convention,
`"BC"_1 = + "R"_1`
`"DC"_2 = -"R"_2`
So Eq.(4) can be written as
`1/f = ("n"_21 -1)(1/"R"_1 - 1/"R"_2).........(5) (∵ "n"_21 = "n"_2/"n"_1)`
Equation (5) is known as the lens maker’s formula. It is useful to design lenses of desired focal length using surfaces of suitable radii of curvature. Note that the formula is true for a concave lens also. In that case R1is negative, R2is positive and therefore, f is negative.
From Eqs. (3) and (4), we get
`"n"_1/"OB" + "n"_1/"DI" = "n"_1/f`...............(6)
Again, in the thin lens approximation, B and D are both close to the optical centre of the lens. Applying the sign convention,
BO = –u, DI = +v,we get
`1/"v"-1/"u"=1/f`.............(7)
Equation (7) is the familiar thin lens formula.
APPEARS IN
RELATED QUESTIONS
What type of wavefront will emerge from a (i) point source, and (ii) distance light source?
A convex lens has a focal length of 10 cm. Find the location and nature of the image if a point object is placed on the principal axis at a distance of (a) 9.8 cm, (b) 10.2 cm from the lens.
A slide projector has to project a 35 mm slide (35 mm × 23 mm) on a 2 m × 2 m screen at a distance of 10 m from the lens. What should be the focal length of the lens in the projector?
An extended object is placed at a distance of 5.0 cm from a convex lens of focal length 8.0 cm. (a) Draw the ray diagram (to the scale) to locate the image and from this, measure the distance of the image from the lens. (b) Find the position of the image from the lens formula and see how close the drawing is to the correct result.
A 5 mm high pin is placed at a distance of 15 cm from a convex lens of focal length 10 cm. A second lens of focal length 5 cm is placed 40 cm from the first lens and 55 cm from the pin. Find (a) the position of the final image, (b) its nature and (c) its size.
Two convex lenses, each of focal length 10 cm, are placed at a separation of 15 cm with their principal axes coinciding. (a) Show that a light beam coming parallel to the principal axis diverges as it comes out of the lens system. (b) Find the location of the virtual image formed by the lens system of an object placed far away. (c) Find the focal length of the equivalent lens. (Note that the sign of the focal length is positive although the lens system actually diverges a parallel beam incident on it.)
Define the term 'focal length of a mirror'.
Region I and II are separated by a spherical surface of a radius of 25 cm. An object is kept in the region I at a distance of 40 cm from the surface. The distance of the image from the surface is ______.
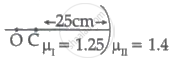
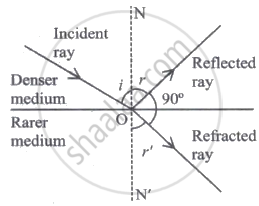
A ray of light from a denser medium strikes a rarer medium at an angle of incidence i as shown in the figure. Refracted and reflected rays make an angle of 90° with each other. The angle of reflection and refraction are r and r'. The critical angle is ______.
A point object in the air is placed symmetrically at a distance of 60 cm in front of a concave spherical surface with a refractive index of 1.5. If the radius of curvature of the surface is 20 cm, find the position of the image formed.
