Advertisements
Advertisements
प्रश्न
Use the above relation to obtain the condition on the position of the object and the radius of curvature in terms of n1and n2 when the real image is formed.
उत्तर

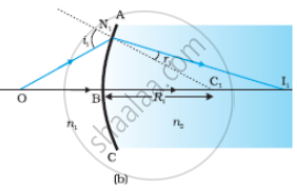
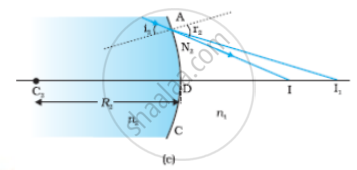
(a) The position of the object, and the image formed by a double convex lens,
(b) Refraction at the first spherical surface and (c) Refraction at the second spherical surface.
Figure (a) shows the geometry of image formation by a double convex lens. The image formation can be seen in terms of two steps: (i) The first refracting surface forms the image I1 of the object O [Fig. (b)]. The image I1 acts as a virtual object for the second surface that forms the image at I [Fig. (c)].
Applying Equation `"n"_2/"v"-"n"_1/"u" = ("n"_2-"n"_1)/"R"` to the first interface ABC,
We get
`"n"_1/"OB" + "n"_2/"BI"_1 = ("n"_2-"n"_1)/"BC"_1` ......(1)
A similar procedure applied to the second interface ADC gives,
`"n"_2/"DI"_1 +"n"_1/"DI" = ("n"_2-"n"_1)/"DC"_1` ......(2)
For a thin lens, BI1= DI1. Adding
Eqs. (1) and (2), we get
`"n"_1/"OB" + "n"_1/"DI" = ("n"_2 - "n"_1)(1/"BC"_1+1/"DC"_2)`.....(3)
Suppose the object is at infinity, i.e., `"OB" -> ∞ and "DI" = f, Eq.(3) "gives"`
`"n"_1/f = ("n"_2-"n"_2)(1/"BC"_1 + 1/"DC"_2) ......(4)`
The point where image of an object placed at infinity is formed is called the focus F, of the lens and the distance f gives its focal length.
By the sign convention,
`"BC"_1 = + "R"_1`
`"DC"_2 = -"R"_2`
So Eq.(4) can be written as
`1/f = ("n"_21 -1)(1/"R"_1 - 1/"R"_2).........(5) (∵ "n"_21 = "n"_2/"n"_1)`
Equation (5) is known as the lens maker’s formula. It is useful to design lenses of desired focal length using surfaces of suitable radii of curvature. Note that the formula is true for a concave lens also. In that case R1is negative, R2is positive and therefore, f is negative.
From Eqs. (3) and (4), we get
`"n"_1/"OB" + "n"_1/"DI" = "n"_1/f`...............(6)
Again, in the thin lens approximation, B and D are both close to the optical centre of the lens. Applying the sign convention,
BO = –u, DI = +v,we get
`1/"v"-1/"u"=1/f`.............(7)
Equation (7) is the familiar thin lens formula.
APPEARS IN
संबंधित प्रश्न
The equation of refraction at a spherical surface is \[\frac{\mu_2}{\nu} - \frac{\mu_1}{\mu} = \frac{\mu_2 - \mu_1}{R}\]
Taking \[R = \infty\] show that this equation leads to the equation
\[\frac{\text{ Real depth }}{\text{ Apparent depth }} = \frac{\mu_2}{\mu_1}\]
for refraction at a plane surface.
A convex lens has a focal length of 10 cm. Find the location and nature of the image if a point object is placed on the principal axis at a distance of (a) 9.8 cm, (b) 10.2 cm from the lens.
A slide projector has to project a 35 mm slide (35 mm × 23 mm) on a 2 m × 2 m screen at a distance of 10 m from the lens. What should be the focal length of the lens in the projector?
An extended object is placed at a distance of 5.0 cm from a convex lens of focal length 8.0 cm. (a) Draw the ray diagram (to the scale) to locate the image and from this, measure the distance of the image from the lens. (b) Find the position of the image from the lens formula and see how close the drawing is to the correct result.
A converging lens of focal length 15 cm and a converging mirror of focal length 10 cm are placed 50 cm apart with common principal axis. A point source is placed in between the lens and the mirror at a distance of 40 cm from the lens. Find the locations of the two images formed.
Define the term 'focal length of a mirror'.
Region I and II are separated by a spherical surface of a radius of 25 cm. An object is kept in the region I at a distance of 40 cm from the surface. The distance of the image from the surface is ______.
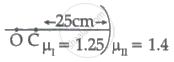
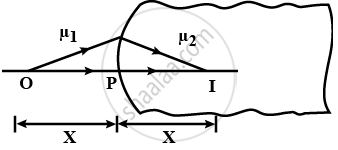
A spherical surface of radius R separates two medium of refractive indices µ1 and µ2, as shown in figure. Where should an object be placed in the medium 1 so that a real image is formed in medium 2 at the same distance?
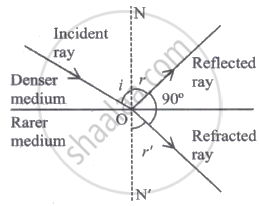
A ray of light from a denser medium strikes a rarer medium at an angle of incidence i as shown in the figure. Refracted and reflected rays make an angle of 90° with each other. The angle of reflection and refraction are r and r'. The critical angle is ______.
Obtain an expression for refraction at a single convex spherical surface, i.e., the relation between μ1 (rarer medium), μ2 (denser medium), object distance u, image distance v and the radius of curvature R.
