Advertisements
Advertisements
Question
A police van moving on a highway with a speed of 30 km h–1 fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h–1. If the muzzle speed of the bullet is 150 m s–1, with what speed does the bullet hit the thief’s car? (Note: Obtain that speed which is relevant for damaging the thief’s car).
Solution
Speed of the police van, vp = 30 km/h = `(30xx100)/3600` = 8.33 m/s
Muzzle speed of the bullet, vb = 150 m/s
Speed of the thief’s car, vt = 192 km/h = `(192xx1000)/3600` = 53.33 m/s
Bullet's speed relative to ground (from police van) = vb + vp
= 150 + 8.33 = 158.33 m/s
Since both vehicles are moving in the same direction, the velocity with which the bullet hits the thief’s car can be obtained as follows:
vbt = vb + vp - vt
= 158.33 - 53.33 = 105 m/s
APPEARS IN
RELATED QUESTIONS
The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively, are shown in the figure. Choose the correct entries in the brackets below;
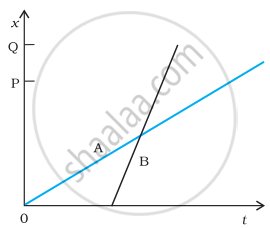
- (A/B) lives closer to the school than (B/A)
- (A/B) starts from the school earlier than (B/A)
- (A/B) walks faster than (B/A)
- A and B reach home at the (same/different) time
- (A/B) overtakes (B/A) on the road (once/twice).
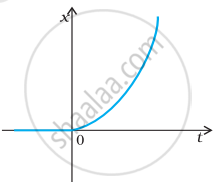
The figure shows the x-t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t < 0 and on a parabolic path for t > 0? If not, suggest a suitable physical context for this graph.
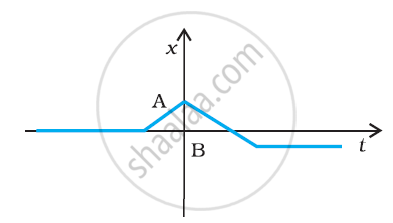
Suggest a suitable physical situation for the following graphs:
Two projectiles A and B are projected with angle of projection 15° for the projectile A and 45° for the projectile B. If RA and RB be the horizontal range for the two projectiles, then
A particle starts from the origin, goes along the X-axis to the point (20 m, 0) and then return along the same line to the point (−20 m, 0). Find the distance and displacement of the particle during the trip.
A ball is dropped and its displacement vs time graph is as shown figure (displacement x is from ground and all quantities are +ve upwards).

- Plot qualitatively velocity vs time graph.
- Plot qualitatively acceleration vs time graph.
A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the (horizontal) distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building? (take g = 10 m/s2)
The velocity-displacement graph of a particle is shown in figure.
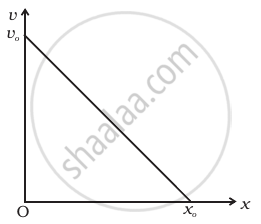
- Write the relation between v and x.
- Obtain the relation between acceleration and displacement and plot it.
Ship A is sailing towards the northeast with velocity `vecv = 30hati + 50hatj` km/hr where `hati` points east and `hatj`, north. Ship B is at a distance of 80 km east and 150 km north of Ship A and is sailing west at 10 km/hr. A will be at the minimum distance from B in ______.
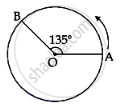
A person moved from A to B on a circular path as shown in figure. If the distance travelled by him is 60 m, then the magnitude of displacement would be: (Given cos135° = - 0.7)