Advertisements
Advertisements
Question
A resistor of 50 Ω, a capacitor of `(25/pi)` µF and an inductor of `(4/pi)` H are connected in series across an ac source whose voltage (in volts) is given by V = 70 sin (100 πt). Calculate:
- the net reactance of the circuit
- the impedance of the circuit
- the effective value of current in the circuit.
Solution
Given:
Resistance (R) = 50 Ω
Capacitor (C) = `25/pi`
Inductance (L) = `4/pi`
V = 70 sin (100 πt)
From this equation, we can identify ω as 100 πt and V as 70 volts.
(a) We can find net reactance from the following formula.
Net reactance, XL + XC
XL = ωL (ω = 100 π, L = 4/π)
`X_L = 100pi xx 4/pi`
`X_L = 400 Omega`
`X_C = 1/(omegaC)` (ω = 100 π, C = 25/π)
`X_C = 1/((100pi xx 25/pi xx 10^-6))`
`X_C = 10^4/25`
`X_C = 400Omega`
Net reactance = (400 + 400) Ω = 800 Ω
(b) Impedance of the circuit
We can find the impedance of the circuit from the following formula:
`Z = sqrt(R^2 + (X_L - X_C)^2)`
Where R is the resistance.
Z = `sqrt((50)^2 + [(400 - 400)^2])`
Z = 50 Ω
(c) Effective value of current
I = `V/Z` (V0 = 70 volt, Z = 50 Ω)
I = `70/(50sqrt2)`
I ≅ 1 A
APPEARS IN
RELATED QUESTIONS
A 2 µF capacitor, 100 Ω resistor and 8 H inductor are connected in series with an AC source.
(i) What should be the frequency of the source such that current drawn in the circuit is maximum? What is this frequency called?
(ii) If the peak value of e.m.f. of the source is 200 V, find the maximum current.
(iii) Draw a graph showing variation of amplitude of circuit current with changing frequency of applied voltage in a series LRC circuit for two different values of resistance R1 and R2 (R1 > R2).
(iv) Define the term 'Sharpness of Resonance'. Under what condition, does a circuit become more selective?
Show that the current leads the voltage in phase by π/2 in an AC circuit containing an ideal capacitor ?
An AC source producing emf ε = ε0 [cos (100 π s−1)t + cos (500 π s−1)t] is connected in series with a capacitor and a resistor. The steady-state current in the circuit is found to be i = i1 cos [(100 π s−1)t + φ1) + i2 cos [(500π s−1)t + ϕ2]. So,
The peak voltage of a 220 V AC source is
Average power supplied to a capacitor over one complete cycle is ______.
A capacitor has capacitance C and reactance X, if capacitance and frequency become double, then reactance will be ______.
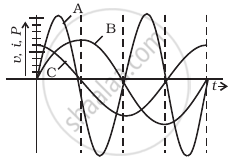
A device ‘X’ is connected to an a.c source. The variation of voltage, current and power in one complete cycle is shown in figure.
- Which curve shows power consumption over a full cycle?
- What is the average power consumption over a cycle?
- Identify the device ‘X’.
Explain why the reactance provided by a capacitor to an alternating current decreases with increasing frequency.
