Advertisements
Advertisements
Question
A rod of negligible heat capacity has length 20 cm, area of cross section 1.0 cm2 and thermal conductivity 200 W m−1°C−1. The temperature of one end is maintained at 0°C and that of the other end is slowly and linearly varied from 0°C to 60°C in 10 minutes. Assuming no loss of heat through the sides, find the total heat transmitted through the rod in these 10 minutes.
Solution
Given:
Length of the rod, l = 20 cm = 0.2 m
Area of cross section of the rod, A = 1.0 cm2 = 1.0 × 10 -4m2
Thermal conductivity of the material of the rod, k = 200 W m-1° C-1
The temperature of one end of the rod is increased uniformly by 60° C within 10 minutes.
This mean that the rate of increase of the temperature of one end is 0.1° C per second
`rArr 60/(10xx60)""^circ C//s`
So, total heat flow can be found by adding heat flow every second.
Rate of flow of heat = `(dQ)/dt`
Q"net" = ∑ `(KA)/d ( T_2 - T_1)×Deltat`
For each interval,
`Deltat = 1`
`Q"net" = KA/d ( 0.1 + (KA)/d xx0.2 + (KA)/d xx0.3 + ...................+ KA/dxx 60.0`
`Q"net" = (KA)/d (0.1 + 0.2 +.........+ 60.0)`
sum of n terms of an AP is given by
`s_n = n/2 ( axxa_n)`
`Q_net = (KA)/d xx 600/2 (0.1+60)`
⇒` Q'"net" = (200xx - 10^-4)/(20xx10^-2) xx 600/2xx60.1`
⇒ Qnet = 1800J (approximately)
APPEARS IN
RELATED QUESTIONS
A bullet of mass 20 g enters into a fixed wooden block with a speed of 40 m s−1 and stops in it. Find the change in internal energy during the process.
A block of mass 100 g slides on a rough horizontal surface. If the speed of the block decreases from 10 m s−1 to 5 m s−1, find the thermal energy developed in the process.
The blocks of masses 10 kg and 20 kg moving at speeds of 10 m s−1 and 20 m s−1respectively in opposite directions, approach each other and collide. If the collision is completely inelastic, find the thermal energy developed in the process.
The thermal conductivity of a rod depends on
One end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
A uniform slab of dimension 10 cm × 10 cm × 1 cm is kept between two heat reservoirs at temperatures 10°C and 90°C. The larger surface areas touch the reservoirs. The thermal conductivity of the material is 0.80 W m−1 °C−1. Find the amount of heat flowing through the slab per minute.
A pitcher with 1-mm thick porous walls contains 10 kg of water. Water comes to its outer surface and evaporates at the rate of 0.1 g s−1. The surface area of the pitcher (one side) = 200 cm2. The room temperature = 42°C, latent heat of vaporization = 2.27 × 106 J kg−1, and the thermal conductivity of the porous walls = 0.80 J s−1 m−1°C−1. Calculate the temperature of water in the pitcher when it attains a constant value.
A metal rod of cross sectional area 1.0 cm2 is being heated at one end. At one time, the temperatures gradient is 5.0°C cm−1 at cross section A and is 2.5°C cm−1 at cross section B. Calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB = 0.40 J°C−1, thermal conductivity of the material of the rod = 200 W m−1°C−1. Neglect any loss of heat to the atmosphere
A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2. The inner surface (a cylinder a length d and radius r1) is maintained at a temperature θ1 and the outer surface (a cylinder of length d and radius r2) is maintained at a temperature θ2 (θ1 > θ2). The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.
A hollow tube has a length l, inner radius R1 and outer radius R2. The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2 (T2 > T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2.
A composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivites K1 and K2. The slabs have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
Suppose the bent part of the frame of the previous problem has a thermal conductivity of 780 J s−1 m−1 °C−1 whereas it is 390 J s−1 m−1°C−1 for the straight part. Calculate the ratio of the rate of heat flow through the bent part to the rate of heat flow through the straight part.
The two rods shown in following figure have identical geometrical dimensions. They are in contact with two heat baths at temperatures 100°C and 0°C. The temperature of the junction is 70°C. Find the temperature of the junction if the rods are interchanged.

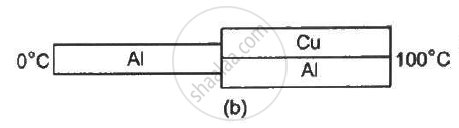
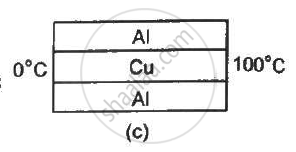
The three rods shown in figure have identical geometrical dimensions. Heat flows from the hot end at a rate of 40 W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b) and in (c). Thermal condcutivities of aluminium and copper are 200 W m−1°C−1 and 400 W m−1°C−1 respectively.

A hollow metallic sphere of radius 20 cm surrounds a concentric metallic sphere of radius 5 cm. The space between the two spheres is filled with a nonmetallic material. The inner and outer spheres are maintained at 50°C and 10°C respectively and it is found that 100 J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the spheres.
