Advertisements
Advertisements
Question
A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the semicircular rod to the heat transferred through a cross section of the straight rod in a given time.
Solution
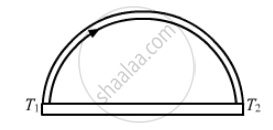
Let A be the area of cross section and K be the thermal conductivity of the material of the rod.
Let q1 be the rate of flow of heat through a semicircular rod.
Rate of flow of heat is given by
`q1 = (dQ) / dt = (K.A (T_1 - T_2 ))/(pi r)`
Let q2 be the rate of flow of heat through a straight rod.
`q_2 = (dQ)/(dt) = (KA (T_1 - T_2))/ (2r)`
Ratio of the rate of flow of heat through the 2 rods
= `(q1)/(q2) =(2r)/(pir) = 2/pi`
APPEARS IN
RELATED QUESTIONS
A metal sheet with a circular hole is heated. The hole
Two identical rectangular strips, one of copper and the other of steel, are riveted together to form a bimetallic strip (acopper> asteel). On heating, this strip will
Find the ratio of the lengths of an iron rod and an aluminium rod for which the difference in the lengths is independent of temperature. Coefficients of linear expansion of iron and aluminium are 12 × 10–6 °C–1 and 23 × 10–6 °C–1 respectively.
An aluminium plate fixed in a horizontal position has a hole of diameter 2.000 cm. A steel sphere of diameter 2.005 cm rests on this hole. All the lengths refer to a temperature of 10 °C. The temperature of the entire system is slowly increased. At what temperature will the ball fall down? Coefficient of linear expansion of aluminium is 23 × 10–6 °C–1 and that of steel is 11 × 10–6 °C–1.
In a room containing air, heat can go from one place to another
A steel frame (K = 45 W m−1°C−1) of total length 60 cm and cross sectional area 0.20 cm2, forms three sides of a square. The free ends are maintained at 20°C and 40°C. Find the rate of heat flow through a cross section of the frame.
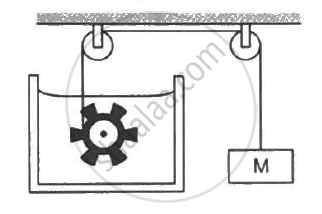
Following Figure shows water in a container having 2.0 mm thick walls made of a material of thermal conductivity 0.50 W m−1°C−1. The container is kept in a melting-ice bath at 0°C. The total surface area in contact with water is 0.05 m2. A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the block goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of 10 cm s−1 and the temperature of the water remains constant at 1.0°C. Find the mass M of the block. Assume that the heat flows out of the water only through the walls in contact. Take g = 10 m s−2.
On a winter day when the atmospheric temperature drops to −10°C, ice forms on the surface of a lake. (a) Calculate the rate of increase of thickness of the ice when 10 cm of the ice is already formed. (b) Calculate the total time taken in forming 10 cm of ice. Assume that the temperature of the entire water reaches 0°C before the ice starts forming. Density of water = 1000 kg m−3, latent heat of fusion of ice = 3.36 × 105 J kg−1and thermal conductivity of ice = 1.7 W m−1°C−1. Neglect the expansion of water of freezing.
A room has a window fitted with a single 1.0 m × 2.0 m glass of thickness 2 mm. (a) Calculate the rate of heat flow through the closed window when the temperature inside the room is 32°C and the outside is 40°C. (b) The glass is now replaced by two glasspanes, each having a thickness of 1 mm and separated by a distance of 1 mm. Calculate the rate of heat flow under the same conditions of temperature. Thermal conductivity of window glass = 1.0 J s−1 m−1°C−1 and that of air = 0.025 m-1°C-1 .
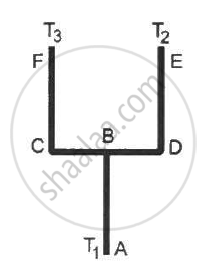
Four identical rods AB, CD, CF and DE are joined as shown in following figure . The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1, T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
A calorimeter of negligible heat capacity contains 100 cc of water at 40°C. The water cools to 35°C in 5 minutes. The water is now replaced by K-oil of equal volume at 40°C. Find the time taken for the temperature to become 35°C under similar conditions. Specific heat capacities of water and K-oil are 4200 J kg−1 K−1 and 2100 J kg−1 K−1respectively. Density of K-oil = 800 kg m−3.
There are two identical vessels filled with equal amounts of ice. The vessels are of different metals. If the ice melts in the two vessels in 20 and 35 minutes respectively, the ratio of the coefficients of thermal conductivity of the two metals is:
We would like to prepare a scale whose length does not change with temperature. It is proposed to prepare a unit scale of this type whose length remains, say 10 cm. We can use a bimetallic strip made of brass and iron each of different length whose length (both components) would change in such a way that difference between their lengths remain constant. If αiron = 1.2 × 10−5/K and αbrass = 1.8 × 10−5/K, what should we take as length of each strip?
A thin rod having length L0 at 0°C and coefficient of linear expansion α has its two ends maintained at temperatures θ1 and θ2, respectively. Find its new length.
