Advertisements
Advertisements
Question
Four identical rods AB, CD, CF and DE are joined as shown in following figure . The length, cross-sectional area and thermal conductivity of each rod are l, A and K respectively. The ends A, E and F are maintained at temperature T1, T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.
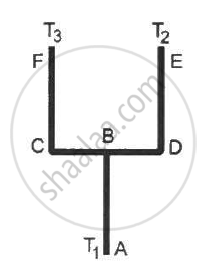
Solution
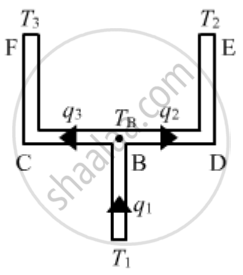
Let the temperature at junction B be T.
Let q1, q2 and q3 be the heat currents, i.e. rate of flow of heat per unit time in AB, BCE and BDF, respectively.
From the diagram, we can see that
q1 = q2 + q3
The rate of flow of heat is given by
`q = (KA DeltaT)/l`
Using this tn the above equation, we get
`(A (T_1 - T))/l = (KA ( T + T_3))/(31/2) + (KA (T-T_2))/(31/2)`
`⇒ T_1 - T = (2(T - T_3))/3+(2(T- T_2))/3`
⇒ 3 (T1 - T) = 2T - 2T3 + 2T - 2T2
`⇒ T = (-3T_1 + 2( T_2 +T_3))/7`
APPEARS IN
RELATED QUESTIONS
Explain why a brass tumbler feels much colder than a wooden tray on a chilly day
Two identical rectangular strips, one of copper and the other of steel, are riveted together to form a bimetallic strip (acopper> asteel). On heating, this strip will
Find the ratio of the lengths of an iron rod and an aluminium rod for which the difference in the lengths is independent of temperature. Coefficients of linear expansion of iron and aluminium are 12 × 10–6 °C–1 and 23 × 10–6 °C–1 respectively.
A glass window is to be fit in an aluminium frame. The temperature on the working day is 40°C and the glass window measures exactly 20 cm × 30 cm. What should be the size of the aluminium frame so that there is no stress on the glass in winter even if the temperature drops to 0°C? Coefficients of linear expansion for glass and aluminium are 9.0 × 10–6 °C–1 and 24 ×100–6°C–1 , respectively.
A steel frame (K = 45 W m−1°C−1) of total length 60 cm and cross sectional area 0.20 cm2, forms three sides of a square. The free ends are maintained at 20°C and 40°C. Find the rate of heat flow through a cross section of the frame.
A cubical box of volume 216 cm3 is made up of 0.1 cm thick wood. The inside is heated electrically by a 100 W heater. It is found that the temperature difference between the inside and the outside surface is 5°C in steady state. Assuming that the entire electrical energy spent appears as heat, find the thermal conductivity of the material of the box.
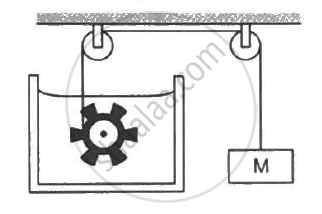
Following Figure shows water in a container having 2.0 mm thick walls made of a material of thermal conductivity 0.50 W m−1°C−1. The container is kept in a melting-ice bath at 0°C. The total surface area in contact with water is 0.05 m2. A wheel is clamped inside the water and is coupled to a block of mass M as shown in the figure. As the block goes down, the wheel rotates. It is found that after some time a steady state is reached in which the block goes down with a constant speed of 10 cm s−1 and the temperature of the water remains constant at 1.0°C. Find the mass M of the block. Assume that the heat flows out of the water only through the walls in contact. Take g = 10 m s−2.
A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the semicircular rod to the heat transferred through a cross section of the straight rod in a given time.
Consider the situation shown in the figure . The frame is made of the same material and has a uniform cross-sectional area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100°C is 130 J.

Following figure shows two adiabatic vessels, each containing a mass m of water at different temperatures. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperatures in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

A calorimeter of negligible heat capacity contains 100 cc of water at 40°C. The water cools to 35°C in 5 minutes. The water is now replaced by K-oil of equal volume at 40°C. Find the time taken for the temperature to become 35°C under similar conditions. Specific heat capacities of water and K-oil are 4200 J kg−1 K−1 and 2100 J kg−1 K−1respectively. Density of K-oil = 800 kg m−3.
There are two identical vessels filled with equal amounts of ice. The vessels are of different metals. If the ice melts in the two vessels in 20 and 35 minutes respectively, the ratio of the coefficients of thermal conductivity of the two metals is:
These days people use steel utensils with copper bottom. This is supposed to be good for uniform heating of food. Explain this effect using the fact that copper is the better conductor.
A thin rod having length L0 at 0°C and coefficient of linear expansion α has its two ends maintained at temperatures θ1 and θ2, respectively. Find its new length.
A cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system?
