Advertisements
Advertisements
Question
A single-square-covered board is a board of 2n x 2n squares in which one square is covered with a single square tile. Show that it is possible to cover this board with triominoes without overlap.
Solution
The size of the board is 2nn x 2n
Number of squares = 2n x 2n = 4n
Number of squares covered = 1
Number of squares to be covered = 4n – 1
4n – 1 is a multiple of 3
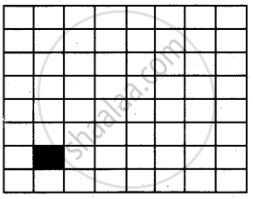
Case 1 : n = 1
The size of the board 2 x 2
one triominoe can cover 3 squares without overlap.
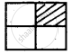
We can cover it with one triominoe and solve the problem.

2 × 2 square Triominoe Triominoe covered square
Case 2 : n ≥ 2
1. place a triamine at the center of the entire board so as to not cover the covered sub-board.
2. One square on the board is covered by a tile. The board has 4 sub-boards of size `2^(2n – 1) xx 2^(2n – 1)`.
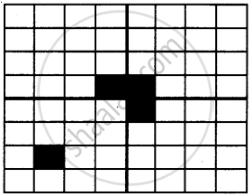
Out of 4 sub-boards, one sub-board is a single square covered sub-board.
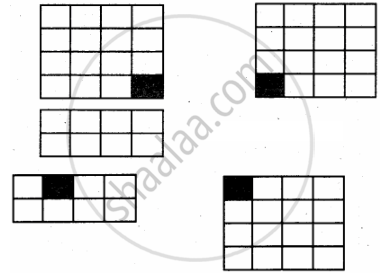
One triominoe can cover the remaining three sub-boards into a single square covered sub-board. The problem of size n is divided into 4 subproblems of size (n – 1). Each sub-board has `2^{2"n" – 1} xx 2^{2"n" – 1} – 1 = 2^{2"n" – 2} – 1 = 4^{"n" – 1} – 1` squares to be covered.
4n – 1 – 1 is also a multiple of 3
In this, the 2n x 2n board is reduced to boards of size 2×2 having are square covered. A triamine can be placed in each of these boards and hence the whole original 2n x 2n. the board is covered with triominoe without overlap.
APPEARS IN
RELATED QUESTIONS
If the Fibonacci number is defined recursively as F(n) = `{(0, "n" = 0), (1, "n" = 1), ("F"("n" - 1),+ "F"("n" - 2) "otherwise"):}`
to evaluate F(4), how many times F() is applied?
Using this recursive definition
`"a"^"n" = {(1, "if" "n" = 0), ("a" × "a"^("n" - 1), "otherwise"):}`
how many multiplications are needed to calculate a10?
What is recursive problem-solving?
Define factorial of a natural number recursively.
Power can also be defined recursively as
`"a"^"n" = {(1, "if" "n" = 0), ("a" × "a"^("n" - 1), "if n is odd"), ("a"^("n""/"2) × "a"^("n""/"2), "if n is even"):}`
Construct a recursive algorithm using this definition. How many multiplications are needed to calculate a10?
Give one reason, why iteration is better than recursion.
Differentiate between direct recursion and indirect recursion.
The following function task() is a part of some class. Assume ‘m’ and ‘n’ are positive integers greater than 0. Answer the questions given below along with dry / run working.
int task(int m, int n)
{ if(m=n)
return m;
else if (m>n)
return task(m-n, n);
else
return task(m, n-m)
}- What will the function task() return when the value of m=30 and n=45?
- What function does task() perform, apart from recursion?
Assertion: Recursion utilises more memory as compared to iteration.
Reason: Time complexity of recursion is higher due to the overhead of maintaining the function call stack.
