Advertisements
Advertisements
Question
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness 2d/3, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
Solution
Initially when there is vacuum between the two plates, the capacitance of the two parallel plates is, ,`C_0 = (epsi_0A)/d` where, A is the area of parallel plates.
Suppose that the capacitor is connected to a battery, an electric field E0 is produced.
Now if we insert the dielectric slab of thickness `t = (2d)/3`the electric field reduces to E.
Now the gap between plates is divided in two parts, for distance t there is electric field E and for the remaining distance (d–t) the electric field is E0.
If V be the potential difference between the plates of the capacitor, then V=Et + E0(d–t)
`V = (2Ed)/3 +E_0 (d-(2d)/3) = (2Ed)/3 +(E_0d)/3 = d/3 (2E + E_0) (because t = d/2)`
`or , V = d/3 ((2E_0)/K + E_0) = (dE_0)/(3K) (K+2) (As,E_0/E = K)`
`Now , E_0 = σ/epsi_0 = q/(epsi_0A) => V = d/(3K) q/(epsi_0A) (K+2)`
`therefore C = q/V = (3K_(epsi_0 A))/(d(K+2))`.
APPEARS IN
RELATED QUESTIONS
Draw a neat labelled diagram of a parallel plate capacitor completely filled with dielectric.
Considering the case of a parallel plate capacitor being charged, show how one is required to generalize Ampere's circuital law to include the term due to displacement current.
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10−3 m2 and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to `(1/2)` QE, where Q is the charge on the capacitor, and E is the magnitude of the electric field between the plates. Explain the origin of the factor `1/2`.
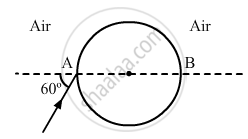
A ray of light falls on a transparent sphere with centre C as shown in the figure. The ray emerges from the sphere parallel to the line AB. Find the angle of refraction at A if the refractive index of the material of the sphere is \[\sqrt{3}\].
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
A parallel-plate capacitor has plate area 20 cm2, plate separation 1.0 mm and a dielectric slab of dielectric constant 5.0 filling up the space between the plates. This capacitor is joined to a battery of emf 6.0 V through a 100 kΩ resistor. Find the energy of the capacitor 8.9 μs after the connections are made.
A parallel plate air condenser has a capacity of 20µF. What will be a new capacity if:
1) the distance between the two plates is doubled?
2) a marble slab of dielectric constant 8 is introduced between the two plates?
Solve the following question.
A parallel plate capacitor is charged by a battery to a potential difference V. It is disconnected from the battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
Two identical capacitors are joined in parallel, charged to a potential V, separated and then connected in series, the positive plate of one is connected to the negative of the other. Which of the following is true?
