Advertisements
Advertisements
Question
A ray of light falls on a transparent sphere with centre C as shown in the figure. The ray emerges from the sphere parallel to the line AB. Find the angle of refraction at A if the refractive index of the material of the sphere is \[\sqrt{3}\].
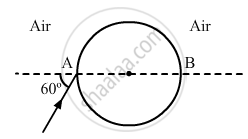
Solution
From Snell's law, we have: \[\frac{\sin\left( i \right)}{\sin\left( r \right)} = \mu\] At A, i = 60° (given)
Now, μ = √3
\[\Rightarrow \sin\left( r \right) = \frac{\sin\left( i \right)}{\mu}\]
\[ \Rightarrow \sin\left( r \right) = \frac{\sin\left( 60° \right)}{\sqrt{3}} = \frac{1}{2}\]
\[ \Rightarrow r = \sin^{- 1} \left( \frac{1}{2} \right)\]
\[ \therefore r = 30°\]
RELATED QUESTIONS
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10−3 m2 and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
A parallel plate capacitor is to be designed with a voltage rating 1 kV, using a material of dielectric constant 3 and dielectric strength about 107 Vm−1. (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i.e., without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed, say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of 50 pF?
A slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor but has a thickness \[\frac{3d}{4}\]. Find the ratio of the capacitance with dielectric inside it to its capacitance without the dielectric.
A slab of material of dielectric constant K has the same area as that of the plates of a parallel plate capacitor but has the thickness d/3, where d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
A parallel-plate capacitor of plate area 40 cm2 and separation between the plates 0.10 mm, is connected to a battery of emf 2.0 V through a 16 Ω resistor. Find the electric field in the capacitor 10 ns after the connections are made.
A parallel plate air condenser has a capacity of 20µF. What will be a new capacity if:
1) the distance between the two plates is doubled?
2) a marble slab of dielectric constant 8 is introduced between the two plates?
Answer the following question.
Describe briefly the process of transferring the charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
For a one dimensional electric field, the correct relation of E and potential V is _________.
In a parallel plate capacitor, the capacity increases if ______.
Two charges – q each are separated by distance 2d. A third charge + q is kept at mid point O. Find potential energy of + q as a function of small distance x from O due to – q charges. Sketch P.E. v/s x and convince yourself that the charge at O is in an unstable equilibrium.
