Advertisements
Advertisements
Question
A solid cylinder has a total surface area of 231 cm2. Its curved surface area is \[\frac{2}{3}\] of the total surface area. Find the volume of the cylinder.
Solution
Given data is as follows:
Total Surface Area = 231 cm2
Curved Surface Area = `2/3 ("Total Surface Area" )`
We have to find the volume of the cylinder.
We have,
Total Surface Area = 231 cm2
`2pirh`+ `2pir^2`=231
Where, `2pirh` is nothing but the Curved Surface Area.
Curved Surface Area = `2/3 ("Total Surface Area" )`
Curved Surface Area= `2/3 xx 231 `=154
Let us replace `2pirh` in the above equation with the value of Curved Surface Area we have just obtained.
154+`2pir^2` =231
`2pir^2` =77
`2 xx 22/7 xx r^2`=77
`r^2 = (77 xx 7)/(2 xx 22 ) = (7xx7)/(2xx2)`
`r = 7/2`
Now, let us find the value of h by using the Curved Surface Area.
Curved Surface Area=154 cm2
`2pirh` =154
Since we know that `r = 7/2` ,
`2 xx 22/7 xx 7/2 xx h` =154
h = 7
Now that we know the value of both h and r , we can easily find the volume of the cylinder.
Volume of the cylinder = `pir^2h`
=`22/7 xx 7/2xx7/2xx7`
`"Volume of the cylinder "= 269.5cm^3`
APPEARS IN
RELATED QUESTIONS
Rukhsar painted the outside of the cabinet, of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?
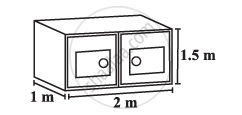
The diameter of roller 1.5 m long is 84 cm. If it takes 100 revolutions to level a playground, find the cost of levelling this ground at the rate of 50 paise per square metre.
Find the volume of a cylinder, the diameter of whose base is 7 cm and height being 60 cm. Also, find the capacity of the cylinder in litres.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. Calculate the ratio of their volumes.
A cylindrical water tank of diameter 1.4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled?
A well with 14 m diameter is dug 8 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embankment. Find the height of the embankment.
The sum of the radius of the base and height of a solid cylinder is 37 m. If the total surface area of the solid cylinder is 1628 cm2. Find the volume of the cylinder.
The height h of a cylinder equals the circumference of the cylinder. In terms of h what is the volume of the cylinder?
A hollow square-shaped tube open at both ends is made of iron. The internal square is of 5 cm side and the length of the tube is 8 cm. There are 192 cm3 of iron in this tube. Find its thickness.
In the example given below, the radius of the base of a cylinder and its height is given. Then find the curved surface area and total surface area.
r = 70 cm, h = 1.4 cm
