Advertisements
Advertisements
Question
A solid sphere and a solid hemisphere have an equal total surface area. Prove that the ratio of their volume is `3sqrt(3):4`
Solution
Total surface area of a sphere = `4pi"r"_1^2` sq.units
Total surface area of a hemisphere = `3pi"r"_2^2` sq.units
Ratio of Total surface area = `4pi"r"_1^2 : 3pi"r"_2^2`
1 = `(4pi"r"_1^2)/(3pi"r"_2^2)` ...(Same Surface Area)
1 = `(4"r"_1^2)/(3"r"_2^2)`
∴ `("r"_1^2)/("r"_2^2) = 3/4`
r12 : r22 = 3 : 4
r1 : r2 = `sqrt(3) : 2`
Ratio of their volume
= `4/3 pi"r"_1^3 : 2/3 pi"r"_2^3`
= `2"r"_1^3 : "r"_2^3`
= `2 xx (sqrt(3))^3` : 23
= `2 xx 3 sqrt(3)` : 8 ...(÷ 2)
= `3sqrt(3) : 4`
Ratio of their volumes = `3sqrt(3) : 4`
Hence it is proved.
APPEARS IN
RELATED QUESTIONS
Find the volume of a sphere whose radius is 7 cm.
`["Assume "pi=22/7]`
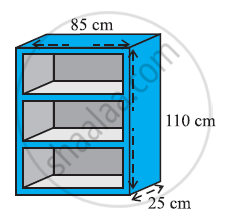
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
Find the volume of a sphere whose radius is 3.5 cm.
A shopkeeper has one laddoo of radius 5 cm. With the same material, how many laddoos of radius 2.5 cm can be made?
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2 : 3.
Volume of a hemisphere is 18000 π cubic cm. Find its diameter.
A spherical ball of radius r1 units is melted to make 8 new identical balls each of radius r2 units. Then r1 : r2 is
A hemispherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 litres per second. How much time will it take to empty the tank completely?
A hemispherical hollow bowl has material of volume cubic `(436π)/3` cubic cm. Its external diameter is 14 cm. Find its thickness
