Advertisements
Advertisements
Question
The outer and the inner surface areas of a spherical copper shell are 576π cm2 and 324π cm2 respectively. Find the volume of the material required to make the shell
Solution
Outer surface area of a spherical shell = 576π cm2
4πR2 = 576π
4 × R2 = 576
R2 = `576/4` = 144
R = `sqrt(144)` = 12 cm
Inner surface area of a spherical shell = 324π cm2
4πr2 = 324π
4r2 = 324
r2 = 81
r = `sqrt(81)` = 9
Volume of the material required = Volume of the hollow hemisphere
= `4/3 pi("R"^3 - "r"^3) "cm"^3`
= `4/3xx 22/7 (12^3 - 9^3) "cm"^3`
= `4/3 xx 22/7 (1728 - 729) "cm"^3`
= `4/3 xx 22/7 xx 999`
= `(4 xx 22 xx 333)/7`
= 4186.29 cm3
Volume of the material required = 4186.29 cm3
APPEARS IN
RELATED QUESTIONS
Find the volume of a sphere whose radius is 7 cm.
`["Assume "pi=22/7]`
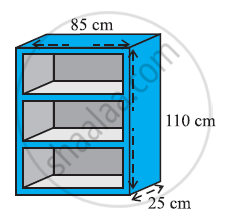
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
A vessel in the form of a hemispherical bowl is full of water. Its contents are emptied in a right circular cylinder. The internal radii of the bowl and the cylinder are 3.5 cm and 7 cm respectively. Find the height to which the water will rise in the cylinder.
A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder
The diameter of a coper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine `("in " mm^3)` is needed to fill this capsule?
A hemispherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties the tank at the rate of 7 litres per second. How much time will it take to empty the tank completely?
The radius of a sphere is 2r, then its volume will be ______.
The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12 m wide and 4 m deep is ______.
