Question

A square lawn has a 2 m wide path surrounding it. If the area of the path is 136 m², find the area of lawn

Answer 1

Let the side of the small lawn = a m

Area of the small square  = a²

Then side of the large lawn = (a + 2(2)) m = (a + 4) m

Area of the large square  = (a + 4)²

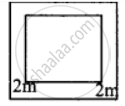
Area of the path = Area of large square – Area of smaller square

136 = (a + 4)² – a²

136 = a² + (2 × a × 4) + 4² – a²

136 = a² + 8a + 16 – a²

136 = 8a + 16

136 = 8(a + 2)

Dividing by 8

17 = a + 2

Subtracting 2 on both sides

17 – 2 = a + 2 – 2

15 = a

∴ side of small square = 15 m

Area of square = (side × side) sq.units

∴ Area of the lawn = (15 × 15) m² = 225 m²

∴ Area of the lawn = 225 m²