Question

A stone is allowed to fall from the top of a tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25 m/s. Calculate when and where the two stones will meet.

Answer 1

Here, h = 100 m

Let the two stones meet after t seconds at point P, which is at a height x above the ground, as shown in the figure.

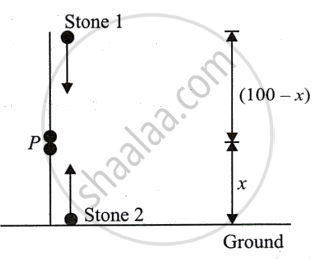
For stone 1,

u = 0, h = (100 - x) m,

a = g = 9.8 m/s²

From s = `ut + 1/2  at^2`

(100 - x) = `0 + 1/2 xx 9.8 t^2`

= 4.9t²         ...(i)

For stone 2,

u = 25 m/s, h = x,

a = - g = - 9.8 m/s²

From s = `ut + 1/2  at^2`

x = `25t + 1/2 (-9.8)t^2`

= 25t - 4.9t²        ...(ii)

Adding equations (i) and (ii)

100 - x + x = 25t

⇒ t = `100/25`

= 4 s

From equation (i),

100 - x = 4.9 × (4)²

100 - x = 78.4

x = 100 - 78.4

x = 21.6 m