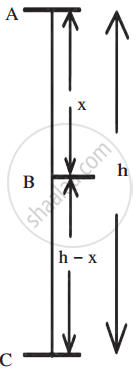
Free Fall

Free Fall

1. At Point A (Height = $h$)

The object is stationary, so:

K.E. = `"1"/"2"` mass x velocity²

K.E. = `"1"/"2"`mν²

K.E. = 0 (since velocity v = 0).

P.E. = mgh (the energy due to its height above the ground).

Total energy:

T.E. = K.E. + P.E.

T.E. = 0 + mgh

T.E. = mgh

2. At Point B (Height = h−x)

The object has fallen a distance $x$ and is now at height h−x. It gains velocity due to gravity.

The velocity at $B$: v²_B=2gx

K.E. at B = `"1"/"2"`mv_B²=`"1"/"2"`m(2gx) 

K.E. = mgx (energy due to motion).

P.E. at B = mg (h-x) (energy due to remaining height).

P.E. = mgh - mgx

Total Energy:

T.E. = K.E. + P.E.

T.E. = mgx + mgh - mgx

T.E. = mgh

3. At Point C (Ground Level, Height = $0$)

The object reaches the ground, so:

u = 0, s = h, a = g

v² = u² + 2as

v²_{C = 0 + 2gh}

K.E. = `"1"/"2"` mv_C²=`"1"/"2"`m(2gh)

K.E. = mgh  (all energy is converted to motion).

The height of the object from the ground at point C is
 h = 0
P.E. = mgh = 0 (no height above ground).

Total Energy:

T.E. = K.E. + P.E.

T.E. = mgh + 0

T.E. = mgh

Conclusion: From the calculations at points $A$, $B$, and $C.$The total energy remains constant throughout the fall.

T.E. = K.E. + P.E. = mgh

As the object falls

• Potential energy decreases as height decreases.
• Kinetic energy increases as velocity increases.

At any point during the fall, the total energy (T.E.) is the sum of P.E. and $.$, and it always equals mgh. This demonstrates the Law of Conservation of Energy, where energy is neither created nor destroyed, only converted between forms.