Lens Formula

The lens formula gives the relationship between the object distance (u), image distance (v), and focal length (f) of a lens:

\[\begin{array}
{cc}1 & 1 \\
\mathbf{v} & \mathbf{u}
\end{array}=\frac{1}{\mathbf{f}}\]

This formula applies to both convex and concave lenses, as long as the sign convention is followed.

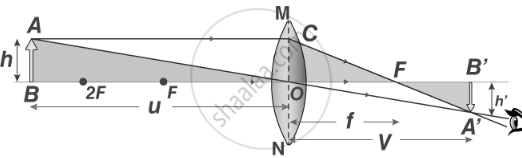
Step 1: Consider a Convex Lens

• Optical center: O
• Focal length: f
• Object: AB placed beyond 2F
• Image: A′B', real, inverted, and smaller

Step 2: Use Similar Triangles

From the image:

1. Triangles △ABO and △A′B′O\triangle △A′B′O are similar:

   \[\frac{A^{\prime}B^{\prime}}{AB}=\frac{OB^{\prime}}{OB}\]

   (Since corresponding angles are equal)

2. Triangles △A′B′F and △OCF are similar:

   \[\frac{A^{\prime}B^{\prime}}{OC}=\frac{FB^{\prime}}{OF}\]

Since OC=AB, we get:

\[\begin{aligned}
\frac{A^{\prime}B^{\prime}}{AB}=\frac{FB^{\prime}}{OF}
\end{aligned}\]

Step 3: Equating the Ratios

\[\frac{OB^{\prime}}{OB}=\frac{FB^{\prime}}{OF}\]

Since OB′=v, OB=u, and OF=f, rewriting:

\[\frac{v}{u}=\frac{v-f}{f}\]

Step 4: Apply Sign Conventions

Using the Cartesian Sign Convention:

• OB = −u (object on the left)
• OB′ = v (image on the right)
• OF = f (focal length)

Rewriting:

\[\frac{v-u}{vu}=\frac{1}{f}\]

\[\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\]

Final Result: Lens Formula

\[\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\]