Topics
Chemical Substances - Nature and Behaviour (Chemistry)
Chemical Reactions and Equations
- Chemical Equation
- Balancing Chemical Equation
- Types of Chemical Change or Chemical Reaction
- Direct Combination (or Synthesis) Reaction
- Decomposition Reactions
- Single Displacement Reactions
- Double Displacement Reaction
- Oxidation, Reduction and Redox Reactions
- Corrosion of Metals
- Rancidity of Food and Its Prevention
World of Living (Biology)
Acids, Bases and Salts
- Acids
- Bases (Alkalis)
- Indicators
- Properties of Acids
- Properties of Bases (Alkalis)
- Acid or a Base in a Water Solution
- Similarities and Differences Between Acids and Bases
- Strength of Acidic or Basic Solutions
- Salts
- Important Salts in Daily Life
- Preparation and Uses of Sodium Hydroxide
- Preparation and Uses of Bleaching Powder
- Preparation and Uses of Baking Soda
- Preparation and Uses of Washing Soda
- Preparation and Uses of Plaster of Paris
Metals and Non Metals
- Types of Element: Metals
- Physical Properties of Metals
- Chemical Properties of Metal
- Types of Element: Non-metal
- Physical Properties of Non-metal
- Chemical Properties of Non-metal
- Ionic or Electrovalent Bond
- Reactivity Series of Metals
- Extraction of Reactive Metals
- Refining of Metals
- Corrosion of Metals
- The Covalent Bond
- Prevention of Corrosion
Natural Phenomena (Physics)
Carbon and its Compounds
- Carbon: a Versatile Element
- The Covalent Bond
- Saturated and Unsaturated Carbon Compounds
- Allotropy and Allotropes of Carbon
- Crystalline Allotropes of Carbon: Diamond
- Crystalline Allotropes of Carbon: Graphite
- Crystalline Allotropes of Carbon: Fullerene
- Chains, Branches and Rings of Carbon Compound
- Functional Groups in Carbon Compounds
- Homologous Series of Carbon Compound
- Nomenclature of Organic Compounds
- Properties of Carbon
- Ethanol
- Ethanoic Acid
- Soap
- Detergents
- Cleansing Action of Soap
Effects of Current (Physics)
Life Processes
- Living Organisms and Life Processes
- Nutrients and Nutrition
- Mode of Nutrition in Plant
- Autotrophic Plants
- Heterotrophic Plants
- Different Ways of Taking Food
- Human Digestive System
- The Mouth and Buccal Cavity
- The Teeth and Its Structure
- The Salivary Glands
- Swallowing and Peristalsis
- The Food Pipe/Oesophagus
- The Stomach
- The Small Intestine
- Pancreas
- Absorption of Food
- The Large Intestine
- Assimilation of Food
- Liver
- Respiration
- Respiration
- Breathing in Other Animals
- Osmoregulation
- Types of Respiration: Aerobic and Anaerobic Respiration
- Human Respiratory System
- Circulation in Animals
- Blood
- Composition of Blood: Plasma (The Liquid Portion of Blood)
- Composition of Blood: Red Blood Cells (Erythrocytes)
- Composition of Blood: White Blood Cells (Leukocytes)
- Composition of Blood: Blood Platelets (Thrombocytes)
- Blood Circulatory System in Human
- Human Heart
- Blood Vessels
- Circulation of Blood in the Heart (Functioning of Heart)
- Types of Closed Circulation
- Heart Beat - Heart Sounds "LUBB" and "DUP"
- Function of Platelets - Clotting of Blood (Coagulation)
- Lymph and Lymphatic System
- Blood Pressure (B.P.)
- Transport System in Plants
- Water absorbing organ
- Translocation of Water (Ascent of Sap)
- Transport of Mineral Ions
- Transport of Food
- Transpiration
- Excretion
- Human Excretory System
- Function of the Kidney - “Production of Urine”
- Excretion
Natural Resources
Periodic Classification of Elements
- History of Periodic Table: Early Attempts at the Classification of Elements
- Dobereiner’s Triads
- Newland's Law of Octaves
- Mendeleev’s Periodic Table
- Merits and Demerits of Mendeleev’s Periodic Table
- The Modern Periodic Table
- Periodic Properties
- Valency
- Atomic Radius Or Atomic Size
- Metallic and Non-metallic Characters
Control and Co-ordination
- Control and Co-ordination in Human Being
- Human Nervous System
- Neuron (Or Nerve Cell) and Its Types
- Neuron (Or Nerve Cell) and Its Types
- Nerve Fibres
- Major Division of the Nervous System
- Central Nervous System (CNS)
- Peripheral Nervous System (PNS)
- The Human Brain - Forebrain
- The Human Brain - Forebrain
- Reflex and Reflex Action
- Nervous Pathways in Reflexes
- Reflex Arc
- Coordination in Plant: Tropism in Plants
- Chemical Coordination
- Plant Hormones
- Types of Plant Hormones: Auxins
- Types of Plant Hormones: Gibberellins
- Types of Plant Hormones: Ethylene
- Types of Plant Hormones: Cytokinins
- Types of Plant Hormones: Abscisic Acid (ABA)
- Types of Plant Hormones: Ethylene
- Hormones in Animals
- Human Endocrine System
- Pituitary Gland or Hypophysis Gland
- Thyroid Gland
- Parathyroid Gland
- Pancreas (Islets of Langerhans)
- Adrenal Gland (Suprarenal Gland)
- Reproductive Glands (Gonads)
- Thymus Gland
Internal assessment
How do Organisms Reproduce?
- Accumulation of Variation During Reproduction
- Reproduction
- Mode of Reproduction in Plant
- Asexual Reproduction in Plant
- Natural Vegetative Reproduction
- Sexual Reproduction in Flowering Plants
- Sexual Reproduction in Animals
- Human Reproduction
- The Male Reproductive System
- The Female Reproductive System
- Menstrual Cycle (Ovarian Cycle)
- Reproductive Health
- Sexually Transmitted Diseases (STD)
Heredity
- Accumulation of Variation During Reproduction
- Heredity or Inheritance
- Gregor Johann Mendel – Father of Genetics
- Monohybrid Cross
- Gregor Johann Mendel – Father of Genetics
- Mendelian Inheritance - Mendel’s Law of Heredity
- Sex Determination
- Organic Evolution
- Lamarck’s Theory of Evolution
- Darwinism
- Theories of Origin of Life
- Speciation
- Evolution and Classiffication
- Evidences for Biological Evolution
- Paleobotany
- Evolution by Stages
- Human Evolution
Light - Reflection and Refraction
- Reflection of Light
- Law of Reflection of Light
- Mirrors
- Plane Mirror
- Spherical Mirrors
- Rules for the Construction of Image Formed by a Spherical Mirror
- Images Formed by Spherical Mirrors
- Concave Mirror
- Image Formation by Concave Mirror
- Convex Mirror
- Image Formation by Convex Mirror
- Sign Convention
- Mirror Equation/Formula
- Linear Magnification (M) Due to Spherical Mirrors
- Introduction to Refraction of Light
- Refraction of Light Through a Rectangular Glass Slab
- Refractive Index
- Spherical Lens
- Images Formed by Sperical Lenses
- Guideline for Image Formation Due to Refraction Through a Convex and Concave Lens
- Concave Lens
- Images Formed by Concave Lenses
- Convex Lens
- Images Formed by Convex Lenses
- Sign Convention
- Lens Formula
- Magnification Due to Spherical Lenses
- Power of a Lens
The Human Eye and the Colourful World
- Human Eye
- Working of the Human Eye
- Eye Defect and Its Correction: Myopia Or Near-sightedness
- Eye Defect and its Correction: Hypermetropia or Far-sightedness
- Eye Defect and Its Correction: Presbyopia
- Care of the Eyes
- Refraction of Light Through a Prism
- Prism
- Dispersion of Light Through Prism and Formation of Spectrum
- Atmospheric Refraction
- Application of Atmospheric Refraction
- Scattering of Light and Its Types
- Applications of Scattering of Light
Electricity
- Electricity
- Electric Current
- Electric Circuit
- Potential and Potential Difference
- Symbols and Functions of Various Components of an Electric Circuits
- Ohm's Law (V = IR)
- Factors Affecting the Resistance of a Conductor
- Electrical Resistivity and Electrical Conductivity
- Resistors in Series
- Resistors in Parallel
- Effects of Electric Current
- Heating Effect of Electric Current
- Electrical Power
Magnetic Effects of Electric Current
- Magnetic Effect of Electric Current
- Magnetic Field
- Properties of magnetic lines of force
- Magnetic Field Due to a Current Carrying Straight Conductor
- Right-hand Thumb Rule
- Magnetic Field Due to Current in a Loop (Or Circular Coil)
- Magnetic Field Due to a Current Carving Cylindrical Coil (or Solenoid)
- Force on a Current Carrying Conductor in a Magnetic Field
- Electric Motor
- Electromagnetic Induction
- Faraday's Laws of Electromagnetic Induction
- Electric Generator
- Alternating Current (A.C.) Generator
- Direct Current Motor
- Household Electrical Circuits
- Distinction Between an A.C. Generator and D.C. Motor
- Types of Current
Our Environment
Sources of Energy
- Source of Energy
- Conventional energy resources or non-renewable energy resources
- Fossil Fuels
- Heat Energy (Thermal Energy)
- Hydroelectric Energy
- Bio-energy
- Wind Energy
- Solar Energy
- Solar Energy Devices
- Energy from the Sea
- Geothermal Energy
- Nuclear Energy
- Nuclear Fission
- Forms of Energy
- Environmental Consequences
- How Long Will an Energy Source Last Us?
Sustainable Management of Natural Resources
- Sustainability of Natural Resources
- Case Study: Ganga Pollution and Ganga Action Plan
- Solid Waste Management
- Five R’s of Waste Management
- Protecting our environment
- Forests: Our Lifeline
- Stakeholders of Forest
- Conservation of Forest
- Conservation of Wildlife
- Water Management (Conservation of Water)
- Fresh Water Management
- Non-crystalline/Amorphous Forms: Coal
- Petroleum
- Conservation of Coal, Petroleum, and Natural Resources
- Overview of Natural Resource Management
- Introduction
- Reflection Formation in a Plane Mirror
- Activity
- Experiment
- Relation Between Mirror Height and Full Image Formation
Introduction:
A plane mirror is a flat and smooth glass surface coated on the back with a thin reflective layer of aluminium or silver. This reflective layer is protected with a coat of materials like lead oxide, which also makes the surface opaque. Plane mirrors are widely used in our daily lives, such as in household mirrors, where we see a clear reflection of ourselves.
- When light rays from a point source hit the mirror, they reflect and reach our eyes. Due to the reflection, these rays appear to be coming from a point behind the mirror, creating the image of the point source. This simple principle of reflection makes plane mirrors essential for forming clear and accurate images.
- The image created by a plane mirror has several unique characteristics: it appears to be the same size as the object, is laterally inverted (left and right are reversed), and is located behind the mirror at the same distance as the object is in front of it.
- Plane mirrors are commonly used in everyday life, such as in bathrooms and dressing rooms, and are essential for understanding basic concepts of light reflection and image formation.
Reflection Formation in a Plane Mirror
Reflection of Light:
As shown in Figure A, light rays falling perpendicular to a mirror are reflected back along the same path. This is due to the laws of reflection, where the angle of incidence equals the angle of reflection.
Image of a Point Source:
In Figure B, a point source O is placed in front of the plane mirror M1M2.
- Light rays OR1 and OR2 hit the mirror and reflect as R1S1 and R2S2, following the laws of reflection.
- When these reflected rays are extended behind the mirror, they appear to meet at O1, forming the virtual image of the point source.
- The reflected rays do not actually meet; hence, the image is virtual and cannot be captured on a screen.
- The distance of the image from the mirror is the same as the distance of the source from the mirror.
Image of an Extended Source:
As shown in Figure C, when an extended source PQ is placed in front of the mirror M1M2:
- The image of P is formed at P1, and the image of Q is formed at Q1.
- Similarly, every point between P and forms corresponding points between P1 and Q1, creating an extended image P1Q1.
Characteristics of the Image:
The image is of the same size as the source, is formed behind the mirror and is virtual.
The image undergoes lateral inversion:
- For example, the word "MIRROR" appears reversed when seen in the mirror.
- Every point on the source is reflected at an equal distance behind the mirror, maintaining symmetry.
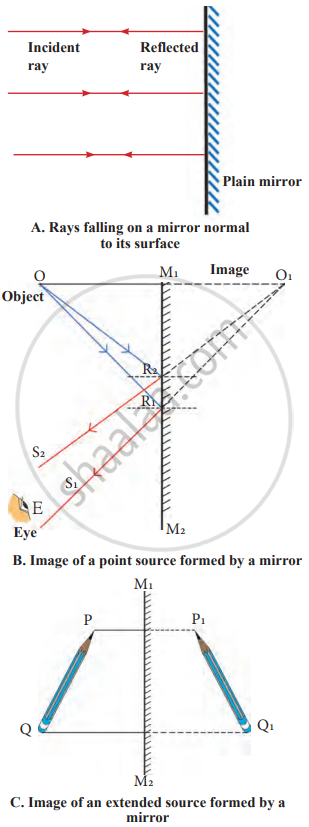
Formation of images by a mirror
Activity
To observe the properties of an image formed by a plane mirror, including its orientation, size, and distance from the mirror.
- Stand in front of a plane mirror and observe your reflection.
- Raise your right hand, and notice that the mirror image raises its left hand. This is called lateral inversion, where left and right appear reversed.
- Move closer to the mirror, and the image also appears to move closer. Move farther, and the image moves farther as well.
- Compare your height with the image in the mirror—it remains the same size as the actual object.
- The image is formed behind the mirror at the same distance as the object is in front of it.
- A plane mirror forms a laterally inverted, same-sized, and virtual image that maintains the same distance from the mirror as the object.

The image in a plane mirror
Experiment
1. Aim: To study the number of images formed by two plane mirrors placed at different angles.
2. Requirements: Two plane mirrors, a small object, and a protractor to measure the angle between the mirrors.
3. Procedure
- Place the two plane mirrors at an angle of 90° to each other.
- Position a small object between the mirrors. Observe and count the number of images formed in the mirrors.
- Change the angle between the mirrors to different values (120°, 60°, 45°, 30°) and count the images for each angle.
\[\begin{gathered}
\mathrm{For~A}=120^\circ{:}n=\frac{360}{120}-1=2 \\
\mathrm{For~A}=90^\circ{:}n=\frac{360}{90}-1=3 \\
\mathrm{For~A}=60^\circ:n=\frac{360}{60}-1=5 \\
\mathrm{For~A}=45^\circ{:}n=\frac{360}{45}-1=7 \\
\mathrm{For~A}=30^{\circ}:n=\frac{360}{30}-1=11
\end{gathered}\]
Use the formula n= \[\mathrm{n}=\frac{360^0}{\mathrm{A}}-1\] , where n is the number of images and A is the angle between the mirrors, to verify the observations. Repeat the experiment with the mirrors placed parallel to each other and count the number of images formed.

Mirrors at right angles to each other
3. Observation Table
|
Angle (°) |
Number of Images |
|---|---|
| 120° | 2 |
| 90° | 3 |
| 60° | 5 |
| 45° | 7 |
| 30° | 11 |
4. Conclusion: The number of images formed by two mirrors increases as the angle between them decreases. When the mirrors are parallel, an infinite number of images are formed. The relationship between the angle and the number of images is consistent with the formula n=\[\mathrm{n}=\frac{360^0}{\mathrm{A}}-1\].
Relation Between Mirror Height and Full Image Formation
Statement: To see the full image of a person standing in front of a mirror, the minimum height of the mirror must be half the height of the person.
Proof:
1. Explanation Using Points
The points on a person are labelled as follows:
- H: Top of the head.
- E: Eyes.
- F: Feet.
R and S are the midpoints of HE and EF, respectively. The mirror P is placed perpendicular to the ground, with the bottom point .
2. Reflection of Light
For the full image to be visible, light rays from the top of the head () and feet () must reflect into the observer’s eyes after striking the mirror. The rays R (from ) and S (from ) must meet the mirror at points that allow perpendicular reflections.
Calculation: The height of the mirror PQ must cover the segments and ES, which are each half of their respective segments:
RE=`"HE"/"2"`
ES=`"EF"/"2"`
Adding these together:
PQ=RE+ES=`"HE"/"2"`+`"EF"/"2"`
=`"HF"/"2"`=Half of the person’s height
Therefore, PQ (the minimum height of the mirror) equals half the height of the person ().
Conclusion: The minimum height of a mirror required to see a person’s full image is half the height of the person. This ensures that the light rays from the top and bottom points of the person reflect properly into the observer's eyes.
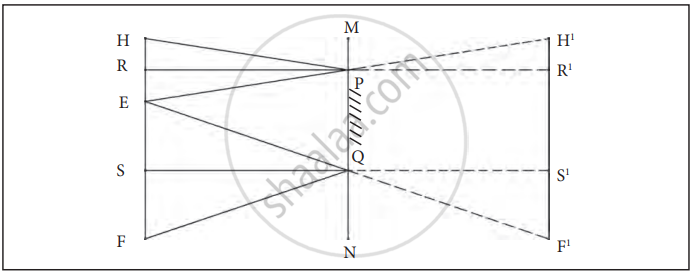
A plane mirror and the full image of a person

