Advertisements
Advertisements
Question
A U-tube containing a liquid is accelerated horizontally with a constant acceleration a0. If the separation between the vertical limbs is l, find the difference in the heights of the liquid in the two arms.
Solution
Let a0 be the acceleration with which U-tube is accelerated horizontally. So, the horizontal part will experience some inertial force.
Also,
pa = Atmospheric pressure
A = Area of cross section
h = Increase in height of the liquid
According to the question,
\[p_a A + A \times l \times \rho \times a_0 = p_a A + h\rho g \times A\]
\[ \Rightarrow hg = a_0 l\]
\[ \Rightarrow h = \frac{a_0 l}{g}\]
APPEARS IN
RELATED QUESTIONS
A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other. What is the specific gravity of spirit?
Does it matter if one uses gauge instead of absolute pressures in applying Bernoulli’s equation? Explain.
A manometer reads the pressure of a gas in an enclosure as shown in Figure (a) When a pump removes some of the gas, the manometer reads as in Figure (b) The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) are poured into the right limb of the manometer? (Ignore the small change in the volume of the gas).

During blood transfusion the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein? [Use the density of whole blood from Table 10.1].
A barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
A one meter long glass tube is open at both ends. One end of the tube is dipped into a mercury cup, the tube is kept vertical and the air is pumped out of the tube by connecting the upper end to a suction pump. Can mercury be pulled up into the pump by this process?
Consider the barometer shown in the following figure. If a small hole is made at a point P in the barometer tube, will the mercury come out from this hole?
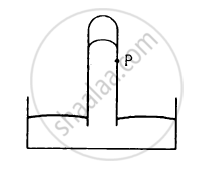
Suppose the pressure at the surface of mercury in a barometer tube is P1 and the pressure at the surface of mercury in the cup is P2.
A barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be ______.
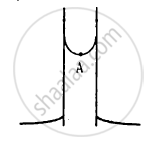
Figure shows a capillary tube of radius r dipped into water. If the atmospheric pressure is P0, the pressure at point A is
Suppose the glass of the previous problem is covered by a jar and the air inside the jar is completely pumped out. (a) What will be the answers to the problem? (b) Show that the answers do not change if a glass of different shape is used provided the height, the bottom area and the volume are unchanged.
Water is filled in a rectangular tank of size 3 m × 2 m × 1 m. (a) Find the total force exerted by the water on the bottom surface on the tank. (b) Consider a vertical side of area 2 m × 1 m. Take a horizontal strip of width δx metre in this side, situated at a depth of x metre from the surface of water. Find the force by the water on this strip. (c) Find the torque of the force calculate in part (b) about the bottom edge of this side.
(d) Find the total force by the water on this side.
(e) Find the total torque by the water on the side about the bottom edge. Neglect the atmospheric pressure and take g = 10 ms−2.
Water leaks out from an open tank through a hole of area 2 mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tanks is 0.4 m2. The pressure at the open surface and at the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. (a) Find the initial speed of water coming out of the hole. (b) Find the speed of water coming out when half of water has leaked out. (c) Find the volume of eater leaked out using a time interval dt after the height remained is h. Thus find the decrease in height dh in terms of h and dt.
(d) From the result of park (c) find the time required for half of the water to leak out.
Considering the pressure p to be proportional to the density, find the pressure p at a height h if the pressure on the surface of the earth is p0.
A glass capillary sealed at the upper end is of length 0.11 m and internal diameter 2 × 10-5 m. This tube is immersed vertically into a liquid of surface tension 5.06 × 10-2 N/m. When the length x × 10-2 m of the tube is immersed in liquid then the liquid level inside and outside the capillary tube becomes the same, then the value of x is ______ m. (Assume atmospheric pressure is 1.01 × 105 `"N"/"m"^2`)
