Advertisements
Advertisements
Question
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm in following figure. The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2. Find the total expenses required for polishing and painting the surface of the bookshelf.

Solution
External length of book shelf = 85cm = l
Breadth= 25cm
Height = 110cm.
External surface area of shelf while leaving front face of shelf
`=lh+2(lb+bh)`
`=[85xx110+21(85xx25+25xx110)]"cm"^2`
`= 19100"cm"^2`
Area of front face = `(85xx110-75xx100+2(75xx5))"cm"^2`
`=1850+ 750"cm"^2`
`=2600"cm"^2`
Area to be polished = `19100+2600"cm"^2`
`=21700"cm"^2`
Cost of polishing `1"cm"^2`"area" = "Rs". 0.20
Cost of polishing `21700"cm"^2 `are `= "Rs".[21700xx0.20]`
`= "Rs". 4340`
Now, length (l), breath (b), height (h) of each row of book shelf is 75cm, 20cm and 30cm
`((110-20)/3)` respectively.
Area to be painted in row `= 2(l+h)b+lh`
`=[2(75+30)xx20+75xx30]"cm"^2`
`=(4200+2250)"cm"^2`
`=6450"cm"^2`
Area to be painted in 3 rows `=(3xx6450)"cm"^2`
`=19350"cm"^2`
`"Cost of painting" 1"cm"^2 area = Rs. 0.10`
`"Cost of painting 19350 area" = Rs.(19350 xx 0 .10) - "Rs".1935`
Total expense required for polishing and painting the surface of the bookshelf
= Rs.(4340 +1935) = Rs. 6275.
APPEARS IN
RELATED QUESTIONS
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and by how much?
The length and breadth of a hall are in the ratio 4: 3 and its height is 5.5 metres. The cost of decorating its walls (including doors and windows) at Rs. 6.60 per square metre is Rs. 5082. Find the length and breadth of the room.
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions is length = 10 m, breadth = 25 dm, height = 50 cm.
How many bricks each of size 25 cm × 10 cm × 8 cm will be required to build a wall 5 m long, 3 m high and 16 cm thick, assuming that the volume of sand and cement used in the construction is negligible?
The external dimensions of a closed wooden box are 48 cm, 36 cm, 30 cm. The box is made of 1.5 cm thick wood. How many bricks of size 6 cm × 3 cm × 0.75 cm can be put in this box?
The length, breadth, and height of a rectangular solid are in the ratio 5: 4: 2. If the total surface area is 1216 cm2, find the length, the breadth, and the height of the solid.
Find the volume and the total surface area of a cuboid, whose :
length = 15 cm, breadth = 10 cm and height = 8 cm.
The areas of any two faces of a cuboid are equal.
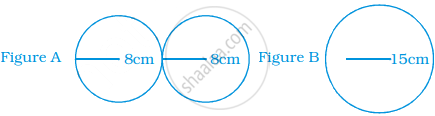
Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?
External dimensions of a closed wooden box are in the ratio 5:4:3. If the cost of painting its outer surface at the rate of Rs 5 per dm2 is Rs 11,750, find the dimensions of the box.
