Advertisements
Advertisements
प्रश्न
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm in following figure. The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2. Find the total expenses required for polishing and painting the surface of the bookshelf.

उत्तर
External length of book shelf = 85cm = l
Breadth= 25cm
Height = 110cm.
External surface area of shelf while leaving front face of shelf
`=lh+2(lb+bh)`
`=[85xx110+21(85xx25+25xx110)]"cm"^2`
`= 19100"cm"^2`
Area of front face = `(85xx110-75xx100+2(75xx5))"cm"^2`
`=1850+ 750"cm"^2`
`=2600"cm"^2`
Area to be polished = `19100+2600"cm"^2`
`=21700"cm"^2`
Cost of polishing `1"cm"^2`"area" = "Rs". 0.20
Cost of polishing `21700"cm"^2 `are `= "Rs".[21700xx0.20]`
`= "Rs". 4340`
Now, length (l), breath (b), height (h) of each row of book shelf is 75cm, 20cm and 30cm
`((110-20)/3)` respectively.
Area to be painted in row `= 2(l+h)b+lh`
`=[2(75+30)xx20+75xx30]"cm"^2`
`=(4200+2250)"cm"^2`
`=6450"cm"^2`
Area to be painted in 3 rows `=(3xx6450)"cm"^2`
`=19350"cm"^2`
`"Cost of painting" 1"cm"^2 area = Rs. 0.10`
`"Cost of painting 19350 area" = Rs.(19350 xx 0 .10) - "Rs".1935`
Total expense required for polishing and painting the surface of the bookshelf
= Rs.(4340 +1935) = Rs. 6275.
APPEARS IN
संबंधित प्रश्न
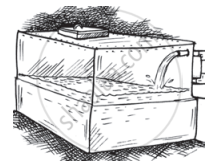
Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of the reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
A cuboidal block of solid iron has dimensions 50 cm, 45 cm and 34 cm. How many cuboids of size 5 cm by 3 cm by 2 cm can be obtained from this block? Assume cutting causes no wastage.
The weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions is length = 10 m, breadth = 25 dm, height = 50 cm.
A swimming pool is 20 m long 15 m wide and 3 m deep. Find the cost of repairing the floor and wall at the rate of Rs 25 per square metre.
The central hall of a school is 80 m long and 8 m high. It has 10 doors each of size 3 m × 1.5 m and 10 windows each of size 1.5 m × 1 m. If the cost of white-washing the walls of the hall at the rate of Rs 1.20 per m2 is Rs 2385.60, fidn the breadth of the hall.
The breadth and height of a rectangular solid are 1.20 m and 80 cm respectively. If the volume of the cuboid is 1.92 m3; find its length.
The internal length, breadth, and height of a closed box are 1 m, 80 cm, and 25 cm. respectively. If its sides are made of 2.5 cm thick wood; find :
(i) the capacity of the box
(ii) the volume of wood used to make the box.
A cube of edge 6 cm and a cuboid with dimensions 4 cm x x cm x 15 cm are equal in volume. Find:
(i) the value of x.
(ii) the total surface area of the cuboid.
(iii) the total surface area of the cube.
(iv) which of these two has a greater surface and by how much?
