Advertisements
Advertisements
Question
एका नदीत, बोटीने प्रवाहाच्या विरुद्ध 36 किमी जाऊन परत त्याच जागी येण्यास प्रतीकला 8 तास लागतात. बोटीचा संथ पाण्यातील वेग ताशी 12 किमी असल्यास नदीच्या प्रवाहाचा वेग काढा.
Advertisements
Solution
समजा, नदीच्या प्रवाहाचा वेग x किमी/तास आहे.
बोटीचा वेग 12 किमी/तास.
प्रवाहाच्या विरुद्ध दिशेला बोटीचा वेग कमी होतो, तसेच प्रवाहाच्या दिशेने तो वाढतो.
बोटीचा वेग पाण्याच्या प्रवाहापेक्षा अधिक आहे.
∴ x < 12
∴ प्रवाहाच्या विरुद्ध दिशेने बोटीचा वेग = (12 - x) किमी/तास
व प्रवाहाच्या दिशेने बोटीचा वेग = (12 + x) किमी/तास
आता, वेळ = `(अंतर)/(वेग)`
प्रवाहाच्या विरुद्ध दिशेने 36 किमी अंतर कापण्यास बोटीला लागलेला वेळ = `36/(12 - x)` तास
प्रवाहाच्या दिशेने 36 किमी अंतर कापण्यास बोटीला लागलेला वेळ = `36/(12 + x)` तास
दिलेल्या अटीनुसार, एकाच ठिकाणी जाऊन परत येण्यासाठी प्रतीकला लागणारा वेळ
∴ `36/(12 - x) + 36/(12 + x) = 8`
∴ `36(1/(12 - x) + 1/(12 + x)) = 8`
∴ `1/(12 - x) + 1/(12 + x) = 8/36`
∴ `((12 + x) + (12 - x))/((12 - x)(12 + x)) = 2/9`
∴ `24/(144 - x^2) = 2/9 ...[(a + b)(a - b) = a^2 - b^2]`
∴ `24 xx 9 = 2(144 - x^2)`
∴ 216 = 288 - 2x2
∴ 2x2 = 288 - 216
∴ 2x2 = 72
∴ x2 = 36
∴ x = ± 6 ...[दोन्ही बाजूंचे वर्गमूळ घेऊन]
परंतु, वेग कधीही ऋण नसतो.
∴ x = 6
∴ नदीच्या प्रवाहाचा वेग 6 किमी/तास आहे.
APPEARS IN
RELATED QUESTIONS
विवेक, हा किशोरपेक्षा 5 वर्षांनी मोठा असून त्यांच्या वयांच्या गुणाकार व्यस्तांची बेरीज `1/6` आहे, तर त्यांची आजची वये काढा.
सुयशला गणिताच्या पहिल्या चाचणीत मिळालेल्या गुणांपेक्षा दुसऱ्या चाचणीत 10 गुण अधिक मिळाले. दुसऱ्या चाचणीतील गुणांची 5 पट ही पहिल्या चाचणीतील गुणांच्या वर्गाइतकी आहे, तर त्याचे पहिल्या चाचणीतील गुण किती?
श्री. कासम यांचा मातीची भांडी बनवण्याचा कुटीर उद्योग आहे. ते दररोज ठरावीक संख्येएवढी भांडी तयार करतात. प्रत्येक भांड्याचे निर्मितीमूल्य, तयार केलेल्या भांड्यांच्या संख्येची 10 पट अधिक ₹ 40 असते. जर एका दिवसातील भांड्यांचे निर्मितीमूल्य ₹ ६०० असेल, तर प्रत्येक भांड्याचे निर्मितीमूल्य व एका दिवसात बनवलेल्या भांड्यांची संख्या काढा.
460 या संख्येला एका नैसर्गिक संख्येने भागल्यास भागाकार भाजकाच्या 5 पटीपेक्षा 6 ने अधिक येत असून बाकी 1 येते, तर भागाकार व भाजक किती?
समलंब मध्ये `square`ABCD मध्ये AB || CD असून त्याचे क्षेत्रफळ 33 चौसेमी आहे, तर आकृतीतील दिलेल्या माहितीवरून चौकोनाच्या चारही बाजूंची लांबी खालील कृती पूर्ण करून काढा.
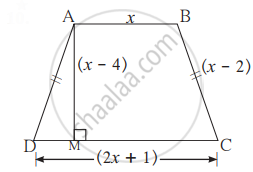
उकल:
`square`ABCD समलंब चौकोन आहे. AB || CD
`"A"(square "ABCD") = 1/2 xx ("AB" + "CD") xx square`
∴ `33 = 1/2(x + 2x + 1) xx square`
∴ `square` = (3x + 1) × `square`
∴ 3x2 + `square` - `square` = 0
∴ 3x (____) + 10 (____) = 0
∴ (3x + 10)(_____) = 0
∴ (3x + 10) = 0 किंवा `square` = 0
∴ x = `- 10/3` किंवा x = `square`
परंतु, लांबी ऋण नसते.
∴ `x ne (- 10)/3` ∴ x = `square`
AB = ______, CD = ______, AD = BC = _______
तळवेल येथील शेतकरी श्री. दिनेश यांच्या आयताकृती शेतीची लांबी ही रुंदीच्या दुपटीपेक्षा 10 मीटरने अधिक आहे. त्यांनी त्या शेतात पावसाचे पाणी पुनर्भरणासाठी शेताच्या रुंदीच्या `1/3` पट बाजू असणाऱ्या चौरसाकृती शेततळ्याची निर्मिती केली. तेव्हा मूळ शेताचे क्षेत्रफळ हे शेततळ्याच्या क्षेत्रफळाच्या 20 पट होते, तर त्या शेताची लांबी आणि रुंदी, तसेच शेततळ्याच्या बाजूची लांबी काढा.
एक टाकी दोन नळांच्या साहाय्याने 2 तासांत पूर्ण भरते. त्यातील फक्त लहान नळाने टाकी भरण्यास लागणारा वेळ, फक्त मोठ्या नळाने टाकी भरण्यास लागणाऱ्या वेळेपेक्षा 3 तास जास्त असतो, तर प्रत्येक नळाने ती टाकी भरण्यास किती वेळ लागतो?
मनीषच्या आईचे आजचे वय त्याच्या वयाच्या 5 पटीपेक्षा 1 ने जास्त आहे. 4 वर्षांपूर्वी त्यांच्या वयांचा गुणाकार 22 असल्यास त्यांची आजची वये काढा.
पाच क्रमागत नैसर्गिक संख्यांच्या वर्गाची बेरीज 1455 आहे, तर त्या संख्या शोधा.
एक टाकी दोन नळाच्या साहाय्याने 6 तासात पूर्ण भरते. ती टाकी भरण्यास लहान नळाला मोठ्या नळापेक्षा 5 तास जास्त लागतात तर प्रत्येक नळाने ती टाकी भरण्यास किती वेळ लागेल?
