Advertisements
Advertisements
Question
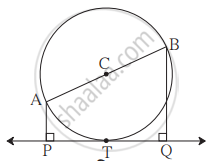
आकृति में, रेख AB बिंदु C केंद्रवाले वृत्त का व्यास है। वृत्त की स्पर्श रेखा PQ वृत्त को बिंदु T पर स्पर्श करती है । रेख AP ⊥ रेखा PQ और रेख BQ ⊥ रेखा PQ तो सिद्ध कीजिए कि, रेख CP ≅ रेख CQ.
Solution
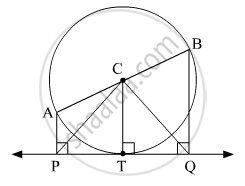
रेख CT, रेख CP और रेख CQ खींचो|
रेख AP ⊥ रेखा PQ ...(दत्त)
रेख CT ⊥ रेखा PQ ...(स्पर्श रेखा-त्रिज्या प्रमेय)
रेख BQ ⊥ रेखा PQ ...(दिया है| )
∴ रेख AP || रेख CT || रेख BQ ...(एक ही रेखा पर खींची गई लंब रेखाएँ समांतर होती हैं |)
∴ `"PT"/"TQ" = "AC"/"CB"` ...(तीन समांतर रेखाएँ तथा उनकी तिर्यक रेखा का गुणधर्म) ...(1)
AC = CB ...(एक ही वृत्त की त्रिज्याएँ)
∴ `"AC"/"CB" = 1` ...(2)
∴ (1) और (2) से,
`"PT"/"TQ" = 1`
∴ PT = TQ ...(3)
ΔCTP और ΔCTQ में,
रेख CT ≅ रेख CT ...(सामान्य भुजा)
∠CTP ≅ ∠CTQ ....(प्रत्येक कोण 90°)
रेख PT ≅ रेख TQ ...[(3) से]
∴ ΔCTP ≅ ΔCTQ ....(सर्वांगसमता की भु-को-भु कसौटी)
∴ रेख CP ≅ रेख CQ ....(स.त्रि.सं.भु.)
APPEARS IN
RELATED QUESTIONS
‘O’ केंद्रवाले वृत्त को रेखा l, बिंदु P पर स्पर्श करती है। यदि वृत्त की त्रिज्या 9 सेमी हो, तो निम्नलिखित प्रश्नों के उत्तर लिखिए :
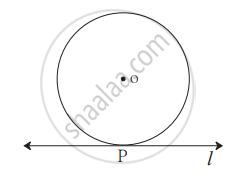
(1) d(O, P) = कितना? क्यों?
(2) यदि d(O, Q) = 8 सेमी हो, तो बिंदु Q का स्थान कहाँ होगा?
(3) d(O, Q) = 15 सेमी, हो तो रेखा l पर बिंदु Q कितनी जगह पर हो सकता है? वे बिंदु P से कितनी दूरी पर होंगे?
संलग्न आकृति में, बिंदु M वृत्त का केंद्र और रेख KL स्पर्श रेखाखंड है | यदि MK = 12, KL = 6√3
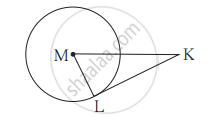
तो -
(1) वृत्त की त्रिज्या ज्ञात कीजिए ।
(2) ∠K और ∠M का माप ज्ञात कीजिए ।
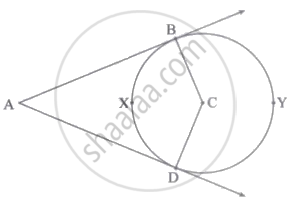
दी गई आकृति में, C केंद्रवाले वृत्त के बाह्य बिंदु A से खींची गई स्पर्श रेखाएँ AB तथा AD हैं। सिद्ध करो कि: ∠A = `1/2` [m(चाप BYD – m(चाप BXD)]