Advertisements
Advertisements
Question
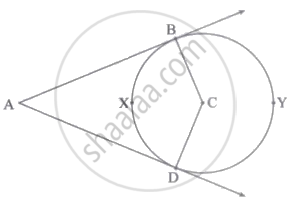
दी गई आकृति में, C केंद्रवाले वृत्त के बाह्य बिंदु A से खींची गई स्पर्श रेखाएँ AB तथा AD हैं। सिद्ध करो कि: ∠A = `1/2` [m(चाप BYD – m(चाप BXD)]
Solution

साध्य: ∠A = `1/2` [m(चाप BYD – m(चाप BXD)]
उपपत्ति:
`{:("रेख" CB ⊥ "रेख" AB),("रेख" CD ⊥ "रेख" AD):}}` ...(स्पर्श रेखा – त्रिज्या लंबता प्रमेय)
∠ABC = ∠ADC = 90° ...(1)
अब, □ABCD में,
∠A + ∠ABC + ∠BCD + ∠ADC = 360° ...(चतुर्भुज के सभी कोणों का योग)
∴ ∠A + 90° + ∠BCD + 90° = 360°
∴ ∠A + ∠BCD = 360° – 180°
∴ ∠A + ∠BCD = 180°
∴ ∠A = 180° – ∠BCD
परंतु, ∠BCD = m(चाप BXD) ...(संगत चाप का केंद्रीय कोण)
∴ ∠A = 180° – m(चाप BXD) ...(2)
अब, m(चाप BXD) + m(चाप BYD) = 360° ...(वृत्त के सभी चापों का योग)
दोनों पक्षों में `1/2` से गुणा करने पर,
`1/2` m(चाप BXD) + `1/2` m(चाप BYD) = `1/2` × 360°
∴ `1/2` m(चाप BXD) + `1/2` m(चाप BYD) = 180° ...(3)
कथन (2) तथा (3) से,
∠A = `1/2` m(चाप BXD) + `1/2` m(चाप BYD) – m(चाप BXD)
∴ ∠A = `1/2` m(चाप BYD) – `1/2` m(चाप BXD)
∴ ∠A = `1/2` m(चाप BYD) – m(चाप BXD)
APPEARS IN
RELATED QUESTIONS
‘O’ केंद्रवाले वृत्त को रेखा l, बिंदु P पर स्पर्श करती है। यदि वृत्त की त्रिज्या 9 सेमी हो, तो निम्नलिखित प्रश्नों के उत्तर लिखिए :
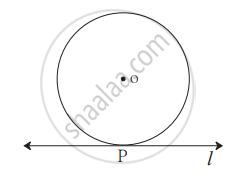
(1) d(O, P) = कितना? क्यों?
(2) यदि d(O, Q) = 8 सेमी हो, तो बिंदु Q का स्थान कहाँ होगा?
(3) d(O, Q) = 15 सेमी, हो तो रेखा l पर बिंदु Q कितनी जगह पर हो सकता है? वे बिंदु P से कितनी दूरी पर होंगे?
संलग्न आकृति में, बिंदु M वृत्त का केंद्र और रेख KL स्पर्श रेखाखंड है | यदि MK = 12, KL = 6√3
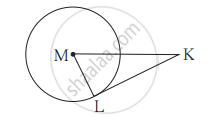
तो -
(1) वृत्त की त्रिज्या ज्ञात कीजिए ।
(2) ∠K और ∠M का माप ज्ञात कीजिए ।
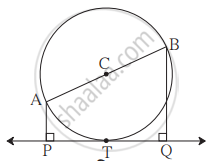
आकृति में, रेख AB बिंदु C केंद्रवाले वृत्त का व्यास है। वृत्त की स्पर्श रेखा PQ वृत्त को बिंदु T पर स्पर्श करती है । रेख AP ⊥ रेखा PQ और रेख BQ ⊥ रेखा PQ तो सिद्ध कीजिए कि, रेख CP ≅ रेख CQ.