Advertisements
Advertisements
Question
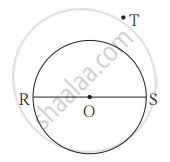
आकृति में रेख RS ; O केंद्रवाले वृत्त का व्यास है। बिंदु T वृत्त के बाह्यभाग में स्थित एक बिंदु है। तो सिद्ध कीजिए ∠RTS एक न्यूनकोण है।
Solution
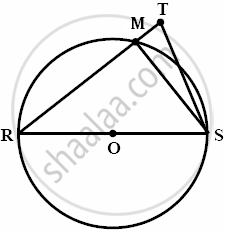
मानो कि, रेख RT यह वृत्त को बिंदु M पर प्रतिच्छेदित करता है |
रेख MS खींचा |
अर्धवृत्त में अंतर्लिखित कोण समकोण है |
∴ ∠RMS = 90°
∴ रेख SM ⊥ भुजा RT
∴ ΔTMS एक समकोण त्रिभुज है |
∴ ∠TMS + ∠MTS + ∠TSM = 180° .........(त्रिभुज के सभी कोणों का योग)
∴ 90° + ∠MTS + ∠TSM = 180°
∴ ∠MTS + ∠TSM = 180° - 90°
∴ ∠MTS + ∠TSM = 90°
∴ ∠MTS < 90°
इस प्रकार, ∠RTS < 90° (R-M-T)
∴ ∠RTS एक न्यूनकोण है | ..........(परिभाषा से)
APPEARS IN
RELATED QUESTIONS
‘O’ केंद्र वाले वृत्त के चाप ACB में ∠ACB अंतर्लिखित किया गया है। यदि m∠ACB = 65° तो m(चाप ACB) = कितना?
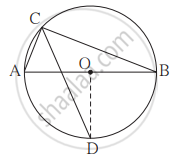
आकृति में, रेख AB बिंदु O केंद्रवाले वृत्त का व्यास है। अंतर्लिखित ∠ACB का समद्विभाजक वृत्त को D बिंदु पर प्रतिच्छेदित करता है। सिद्ध कीजिए कि रेख AD ≅ रेख BD। नीचे दी गई उपपत्ति में रिक्त स्थान की पूर्ति कर पूर्ण कीजिए।
उपपत्ति : रेख OD खींचिए।
∠ACB = `square` (अर्धवृत्त में अंतर्लिखित कोण)
∠DCB = `square` (रेख CD, ∠C का समद्विभाजक है)
m(चाप DB) = `square` (अंतर्लिखित कोण का प्रमेय)
∠DOB = `square` (चाप के माप की परिभाषा) (I)
रेख OA ≅ रेख OB..........(`square`) (II)
∴ रेखा OD रेख AB की `square` रेखा है। (I) तथा (II) से
∴ रेखा AD ≅ रेख BD