Advertisements
Advertisements
Question
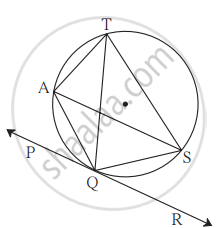
आकृति में, रेखा PR वृत्त को Q बिंदु पर स्पर्श करती है। आकृति के आधार पर निम्नलिखित प्रश्नों के उत्तर लिखिए।
(1) ∠TAQ और ∠TSQ के मापों का योगफल कितना होगा?
(2) ∠AQP के सर्वांगसम कोण का नाम बताइए।
(3) ∠QTS के सर्वांगसम कोण का नाम बताइए।
(4) यदि ∠TAS = 65°, तो ∠TQS और चाप TS के माप बताइए।
(5) यदि ∠AQP = 42° और ∠SQR = 58°, तो ∠ATS के माप ज्ञात कीजिए।
Solution
(1) `square` TAQS चक्रीय चतुर्भुज है .........(परिभाषा से)
चक्रीय चतुर्भुज के प्रमेय से,
∠TAQ + ∠TSQ = 180°.
(2) ∠ATQ तथा ∠ASQ दोनों ∠AQP के सर्वांगसम है | ....(स्पर्श रेखा-छेदन रेखा प्रमेय)
(3) वृत्त के एक ही चाप में अंतर्लिखित सभी कोण सर्वांगसम होते हैं |
∴ ∠QAS ≅ ∠QTS.
∠SQR ≅ ∠QTS. ................(स्पर्श रेखा-छेदन रेखा प्रमेय)
(4) वृत्त के एक ही चाप में अंतर्लिखित सभी कोण सर्वांगसम होते हैं |
∴ ∠TQS ≅ ∠TAS
∴ ∠TQS = 65°
∠TAS = `1/2`m(चाप TS) ...........(अंतर्लिखित कोण प्रमेय से)
∴ 65° = `1/2`m(चाप TS)
∴ m(चाप TS) = 65° × 2
∴ m(चाप TS) = 130°.
(5) ∴ `{:(∠"AQP" = ∠"ATQ" = 42°),(और ∠"QTS" = ∠"SQR" = 58°):}}` ............(स्पर्श रेखा-छेदन रेखा प्रमेय)
∠ATS = ∠ATQ + ∠QTS ..........(कोणों के मापों का योग गुणधर्म)
∴ ∠ATS = `42^circ + 58^circ`
∴ ∠ATS = 100°.
APPEARS IN
RELATED QUESTIONS
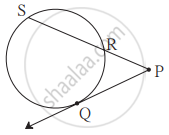
आकृति में, बिंदु Q एक स्पर्शबिंदु है। यदि PQ = 12, PR = 8, तो PS = कितना? RS = कितना?
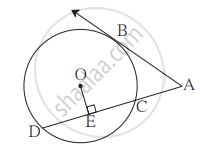
आकृति में, बिंदु B स्पर्श बिंदु और ‘O’ वृत्त का केंद्र है। रेख OE ⊥ रेख AD, AB = 12, AC = 8 तो (1) AD (2) DC और (3) DE = ज्ञात कीजिए।
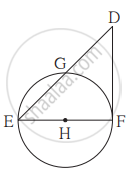
आकृति में, रेख EF व्यास और रेख DF स्पर्श रेखाखंड है। वृत्त की त्रिज्या r हो, तो सिद्ध कीजिए - DE × GE = 4r2
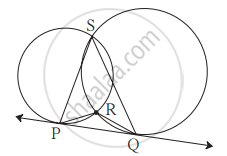
आकृति में दो वृत्त परस्पर बिंदु S तथा बिंदु R पर प्रतिच्छेदित करते हैं। रेखा PQ उन वृत्तों की सामान्य स्पर्श रेखा है जो उन्हे बिंदु P तथा Q पर स्पर्श करती है। सिद्ध कीजिए कि - ∠PRQ + ∠PSQ = 180°
संलग्न आकृति में बिंदु P एक स्पर्श बिंदु है।
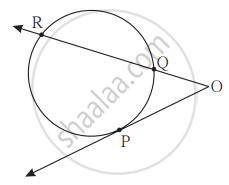
(1) m(चाप PR) = 140°, ∠POR = 36° तो m(चाप PQ) = कितना?
(2) OP = 7.2, OQ = 3.2, तो OR तथा QR ज्ञात कीजिए।
(3) OP = 7.2, OR = 16.2, तो QR का मान कितना?