Advertisements
Advertisements
Question
आकृति में, यदि PQRS एक समांतर चतुर्भुज है तथा AB || PS है, तो सिद्ध कीजिए कि OC || SR है।
Advertisements
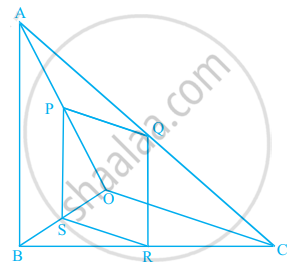
Solution
प्रश्न के अनुसार,
PQRS एक समांतर चतुर्भुज है,
इसलिए, PQ || SR and PS || QR.
AB || PS भी दिया है।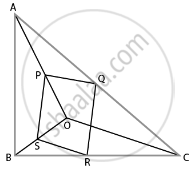
साबित करने के लिए:
OC || SR
∆OPS और OAB से,
PS || AB
∠POS = ∠AOB ...[उभयनिष्ठ कोण]
∠OSP = ∠OBA ...[संगत कोण]
∴ ∆OPS ∼ ∆OAB ...[AAA समानता मानदंड द्वारा]
फिर,
मूल आनुपातिकता प्रमेय का उपयोग करना,
हम पाते हैं,
`("PS")/("AB") = ("OS")/("OB")` ...(i)
∆CQR और ∆CAB से,
QR || PS || AB
∠QCR = ∠ACB ...[उभयनिष्ठ कोण]
∠CRQ = ∠CBA ...[संगत कोण]
∴ ∆CQR ∼ ∆CAB
फिर, मूल आनुपातिकता प्रमेय द्वारा,
`("QR")/("AB") = ("CR")/("CB")`
⇒ `("PS")/("AB") = ("CR")/("CB")` ...(ii) [PS ≅ QR Since, PQRS एक समांतर चतुर्भुज है]
समीकरण (i) और (ii) से,
`("OS")/("OB") = ("CR")/("CB")`
या
`("OB")/("OS") = ("CB")/("CR")`
L.H.S और R.H.S में से 1 घटाने पर, हमें प्राप्त होता है,
`("OB")/("OS") - 1 = ("CB")/("CR") - 1`
⇒ `("OB" - "OS")/("OS") = ("CB" - "CR")/("CR")`
⇒ `("BS")/("OS") = ("BR")/("CR")`
SR || OC ...[बुनियादी आनुपातिकता प्रमेय के विपरीत]
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
आकृति में, DE || BC है। EC ज्ञात कीजिए:
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
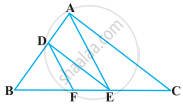
आकृति में DE || AC और DF || AE हैं। सिद्ध कीजिए कि `"BF"/"FE" = "BE"/"EC"` है।
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं)।
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि `"QS"/"SR" = "PQ"/"PR"` है।
यदि ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm और BC = 15 cm है, तो PR बराबर ______ है।
किसी त्रिभुज PQR की भुजाओं PQ और PR पर क्रमश : बिंद A और B इस प्रकार स्थित हैं कि PQ = 12.5 cm, PA = 5 cm, BR = 6 cm और PB = 4 cm हैं। क्या AB || QR है? अपने उत्तर के लिए कारण दीजिए।
दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात `3/5` है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनपात `6/5` है? क्यों?
सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर, उसकी अन्य दो भुजाओं को प्रतिच्छेद करने के लिए, रेखा खींची जाए, तो ये दोनों भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
