Advertisements
Advertisements
Question
आकृति में, DE || BC है। AD ज्ञात कीजिए:
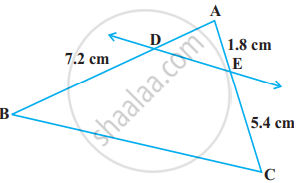
Solution
यह दिया गया है कि DE || BC
मूल आनुपातिकता सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
`("AD")/("DB")=("AE")/("EC")`
`("AD")/7.2=1.8/5.4`
AD × 5.4 = 1.8 × 7.2
AD = `(1.8 xx 7.2)/5.4`
= `18/10xx 72/10 xx10/54`
= `24/10`
= 2.4
∴ AD = 2.4 cm
APPEARS IN
RELATED QUESTIONS
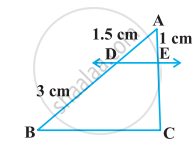
आकृति में, DE || BC है। EC ज्ञात कीजिए:
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
आकृति में यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि `"AM"/"AB" = "AN"/"AD"` है।

आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।(याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
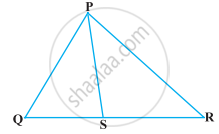
आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि `"QS"/"SR" = "PQ"/"PR"` है।
यह दिया है कि `(BC)/(QR) = 1/3` के साथ ΔABC ~ ΔPQR, है। तब `(ar(PRQ))/(ar(BCA))` बराबर ______ है।
सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर, उसकी अन्य दो भुजाओं को प्रतिच्छेद करने के लिए, रेखा खींची जाए, तो ये दोनों भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
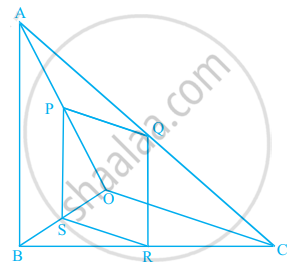
आकृति में, यदि PQRS एक समांतर चतुर्भुज है तथा AB || PS है, तो सिद्ध कीजिए कि OC || SR है।