Advertisements
Advertisements
Question
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
Solution
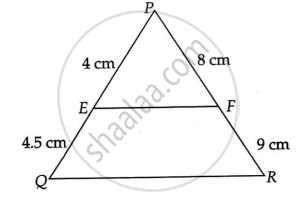
दिया है,
PE = 4 cm
QE = 4.5 cm
PF = 8 cm
RF = 9 cm
⇒ `"PE"/"QE" = 4/4.5 = 40/45 = 8/9`
⇒ `"PF"/"RF" = 8/9`
⇒ `"PE"/"QE" = "PF"/"FR"`
इसलिए, EF, QR के समांतर है।
APPEARS IN
RELATED QUESTIONS
आकृति में, DE || BC है। EC ज्ञात कीजिए:
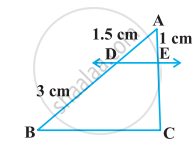
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
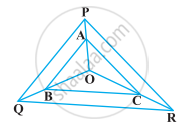
आकृति में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।(याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
ABCD एक समलंब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि `"AO"/"BO" = "CO"/"DO"` है।
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
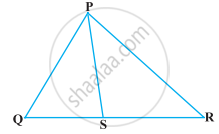
आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि `"QS"/"SR" = "PQ"/"PR"` है।
यह दिया है कि `(BC)/(QR) = 1/3` के साथ ΔABC ~ ΔPQR, है। तब `(ar(PRQ))/(ar(BCA))` बराबर ______ है।
दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात `3/5` है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनपात `6/5` है? क्यों?
