Advertisements
Advertisements
Question
ABCD एक समलंब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि `"AO"/"BO" = "CO"/"DO"` है।
Solution
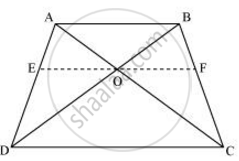
बिंदु O से होकर एक रेखा EF खींचिए, जैसे कि EF || CD
ΔADC में, EO || CD
मूल आनुपातिकता सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
`("AE")/("ED") = ("AO")/("OC")` ...(1)
ΔABD में, OE || AB
अतः, मूल आनुपातिकता सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
`("ED")/("AE") = ("OD")/("BO")`
⇒ `("AE")/("ED") = ("BO")/("OD")` ...(2)
समीकरण (1) और (2) से, हम प्राप्त करते हैं
⇒ `("AO")/("OC") = ("BO")/("OD")`
⇒ `("AO")/("BO") = ("OC")/("OD")`
APPEARS IN
RELATED QUESTIONS
आकृति में, DE || BC है। AD ज्ञात कीजिए:
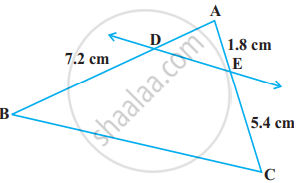
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
आकृति में DE || AC और DF || AE है। सिद्ध कीजिए कि `"BF"/"FE" = "BE"/"EC"` है।
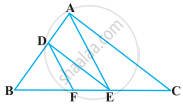
आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।(याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
ΔDEF ~ ΔRPQ दिया है। क्या कहना सत्य है कि ∠D = ∠R और ∠F = ∠P? क्यों?
आकृति में BD और CE परस्पर बिंद P पर प्रतिच्छेद करते हैंक्या ΔPBC ~ ΔPDE है? क्यों?
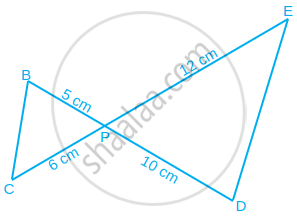
दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात `3/5` है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनपात `6/5` है? क्यों?
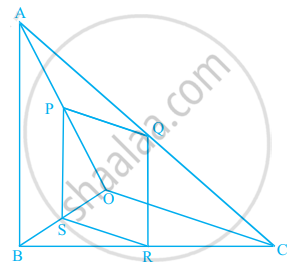
आकृति में, यदि PQRS एक समांतर चतुर्भुज है तथा AB || PS है, तो सिद्ध कीजिए कि OC || SR है।