Advertisements
Advertisements
प्रश्न
आकृति में, DE || BC है। AD ज्ञात कीजिए:
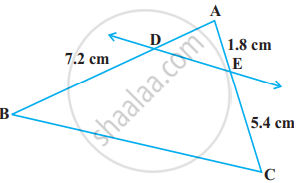
उत्तर
यह दिया गया है कि DE || BC
मूल आनुपातिकता सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
`("AD")/("DB")=("AE")/("EC")`
`("AD")/7.2=1.8/5.4`
AD × 5.4 = 1.8 × 7.2
AD = `(1.8 xx 7.2)/5.4`
= `18/10xx 72/10 xx10/54`
= `24/10`
= 2.4
∴ AD = 2.4 cm
APPEARS IN
संबंधित प्रश्न
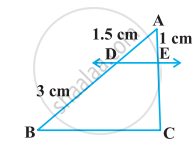
आकृति में, DE || BC है। EC ज्ञात कीजिए:
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
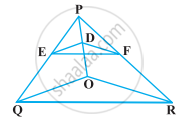
आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं)।
ΔDEF ~ ΔRPQ दिया है। क्या कहना सत्य है कि ∠D = ∠R और ∠F = ∠P? क्यों?
आकृति में BD और CE परस्पर बिंद P पर प्रतिच्छेद करते हैंक्या ΔPBC ~ ΔPDE है? क्यों?
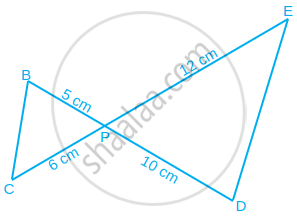
क्या निम्नलिखित कथन सत्य है? क्यों?
“दो चतर्भज समरूप होते हैं. यदि उनके संगत कोण बराबर हों”
सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर, उसकी अन्य दो भुजाओं को प्रतिच्छेद करने के लिए, रेखा खींची जाए, तो ये दोनों भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
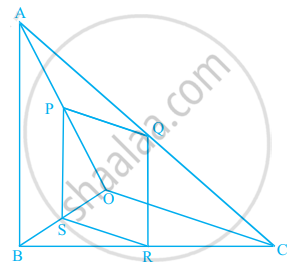
आकृति में, यदि PQRS एक समांतर चतुर्भुज है तथा AB || PS है, तो सिद्ध कीजिए कि OC || SR है।