Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर, उसकी अन्य दो भुजाओं को प्रतिच्छेद करने के लिए, रेखा खींची जाए, तो ये दोनों भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
उत्तर
दिया गया है: मान लीजिए कि एक ΔABC है जिसमें BC के समानांतर एक रेखा DE, AB को D पर और AC को E पर प्रतिच्छेद करती है।
सिद्ध करने के लिए: DE दोनों पक्षों को समान अनुपात में विभाजित करता है।
`("AD")/("DB") = ("AE")/("EC")`
रचना: BE, CD को मिलाएँ और EF ⊥ AB और DG ⊥ AC बनाएँ।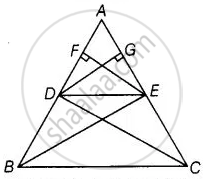
प्रमाण: यहाँ,
त्रिभुज का क्षेत्रफल = `1/2` × आधार × ऊँचाई
ΔADE का क्षेत्रफल = `1/2` × AD × EF
या
ΔADE का क्षेत्रफल = `1/2` × AE × DG
इसी प्रकार,
ΔBDE का क्षेत्रफल = `1/2` × DB × EF
ΔDEC का क्षेत्रफल = `1/2` × EC × DG
`"ar(ΔADE)"/"ar(ΔBDE)" = (1/2 × "AD" × "EF")/(1/2 × "DB" × "EF")`
`"ar(ΔADE)"/"ar(ΔBDE)" = "AD"/"DB"` ...(1)
(2) और (4) से,
`"ar(ΔADE)"/"ar(ΔDEC)" = (1/2 × "AE" × "DG")/(1/2 × "EC" × "DG")`
`"ar(ΔADE)"/"ar(ΔDEC)" = "AE"/"EC"` ...(2)
चूँकि, ΔBDE और ΔDEC एक ही समानांतर DE और BC के बीच और एक ही आधार DE पर स्थित हैं।
∴ ar(ΔBDE) = ar(ΔDEC) ...(3)
(1), (2) और (3) से, हमें प्राप्त होता है,
`"AD"/"BD" ="AE"/"EC"`
अत: सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
आकृति में यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि `"AM"/"AB" = "AN"/"AD"` है।

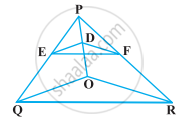
आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं)।
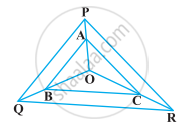
आकृति में क्रमशः OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB || PQ और AC || PR है। दर्शाइए कि BC || QR है।
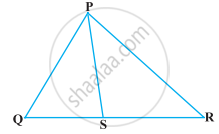
आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि `"QS"/"SR" = "PQ"/"PR"` है।
यह दिया है कि `(BC)/(QR) = 1/3` के साथ ΔABC ~ ΔPQR, है। तब `(ar(PRQ))/(ar(BCA))` बराबर ______ है।
किसी त्रिभुज PQR की भुजाओं PQ और PR पर क्रमश : बिंद A और B इस प्रकार स्थित हैं कि PQ = 12.5 cm, PA = 5 cm, BR = 6 cm और PB = 4 cm हैं। क्या AB || QR है? अपने उत्तर के लिए कारण दीजिए।
सिद्ध कीजिए कि समबाहु त्रिभुज के सभी कोण न्यून कोण होते हैं।
