Advertisements
Advertisements
प्रश्न
आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि `"QS"/"SR" = "PQ"/"PR"` है।
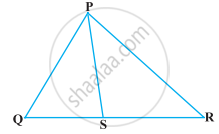
उत्तर
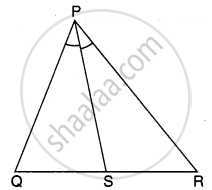
ज्ञात है: ∆PQR में शीर्ष कोण ∠QPR का समद्विभाजक PS, आधार QR को S बिन्दु पर प्रतिच्छेद करता है।
रचना: QP को आगे बढ़ाया। बिन्दु R से TR || PS रेखाखण्ड खींचा जो QP को बिन्दु T पर प्रतिच्छेद करता है (देखिए आकृति)।
चूँकि PS || TR को QT तिर्यक रेखा प्रतिच्छेद करती है।
⇒ ∠QPS = ∠PTR …(1)
चूँकि PS || TR को तिर्यक रेखा PR प्रतिच्छेद करती है।
⇒ ∠SPR = ∠PRT …(2) [एकान्तर कोण हैं।]
⇒ ∠QPS = ∠SPR …(3)
⇒ [PS, ∠QPR का समद्विभाजक दिया है]
⇒ ∠PTR = ∠PRT [समीकरण (1), (2) एवं (3) से]
⇒ PT = PR …(4) [समान कोणों की सम्मुख भुजाएँ हैं|
अब ∆QRT में, PS || TR
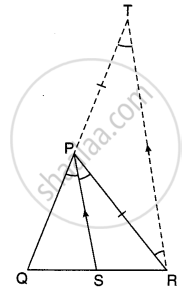
⇒ `"QS"/"SR" = "PQ"/"PT"` ..........[प्रमेय 6.1 से]
⇒ `"QS"/"SR" = "PQ"/"PR"` ........[∵ PT = PR समीकरण (4) से]
इति सिद्धम्
APPEARS IN
संबंधित प्रश्न
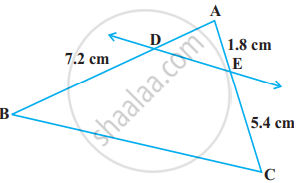
आकृति में, DE || BC है। AD ज्ञात कीजिए:
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
आकृति में DE || AC और DF || AE है। सिद्ध कीजिए कि `"BF"/"FE" = "BE"/"EC"` है।
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
यह दिया है कि `(BC)/(QR) = 1/3` के साथ ΔABC ~ ΔPQR, है। तब `(ar(PRQ))/(ar(BCA))` बराबर ______ है।
ΔDEF ~ ΔRPQ दिया है। क्या कहना सत्य है कि ∠D = ∠R और ∠F = ∠P? क्यों?
किसी त्रिभुज PQR की भुजाओं PQ और PR पर क्रमश : बिंद A और B इस प्रकार स्थित हैं कि PQ = 12.5 cm, PA = 5 cm, BR = 6 cm और PB = 4 cm हैं। क्या AB || QR है? अपने उत्तर के लिए कारण दीजिए।
दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात `3/5` है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनपात `6/5` है? क्यों?
सिद्ध कीजिए कि समबाहु त्रिभुज के सभी कोण न्यून कोण होते हैं।
