Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा के समांतर, उसकी अन्य दो भुजाओं को प्रतिच्छेद करने के लिए, रेखा खींची जाए, तो ये दोनों भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
उत्तर
दिया गया है: मान लीजिए कि एक ΔABC है जिसमें BC के समानांतर एक रेखा DE, AB को D पर और AC को E पर प्रतिच्छेद करती है।
सिद्ध करने के लिए: DE दोनों पक्षों को समान अनुपात में विभाजित करता है।
`("AD")/("DB") = ("AE")/("EC")`
रचना: BE, CD को मिलाएँ और EF ⊥ AB और DG ⊥ AC बनाएँ।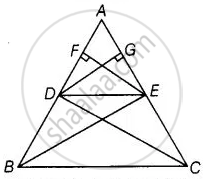
प्रमाण: यहाँ,
त्रिभुज का क्षेत्रफल = `1/2` × आधार × ऊँचाई
ΔADE का क्षेत्रफल = `1/2` × AD × EF
या
ΔADE का क्षेत्रफल = `1/2` × AE × DG
इसी प्रकार,
ΔBDE का क्षेत्रफल = `1/2` × DB × EF
ΔDEC का क्षेत्रफल = `1/2` × EC × DG
`"ar(ΔADE)"/"ar(ΔBDE)" = (1/2 × "AD" × "EF")/(1/2 × "DB" × "EF")`
`"ar(ΔADE)"/"ar(ΔBDE)" = "AD"/"DB"` ...(1)
(2) और (4) से,
`"ar(ΔADE)"/"ar(ΔDEC)" = (1/2 × "AE" × "DG")/(1/2 × "EC" × "DG")`
`"ar(ΔADE)"/"ar(ΔDEC)" = "AE"/"EC"` ...(2)
चूँकि, ΔBDE और ΔDEC एक ही समानांतर DE और BC के बीच और एक ही आधार DE पर स्थित हैं।
∴ ar(ΔBDE) = ar(ΔDEC) ...(3)
(1), (2) और (3) से, हमें प्राप्त होता है,
`"AD"/"BD" ="AE"/"EC"`
अत: सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।(याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
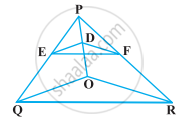
ABCD एक समलंब है जिसमें AB || DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि `"AO"/"BO" = "CO"/"DO"` है।
यह दिया है कि `(BC)/(QR) = 1/3` के साथ ΔABC ~ ΔPQR, है। तब `(ar(PRQ))/(ar(BCA))` बराबर ______ है।
यदि ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm और BC = 15 cm है, तो PR बराबर ______ है।
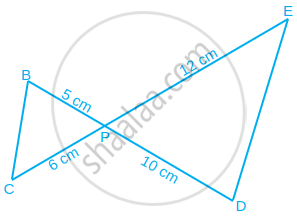
आकृति में BD और CE परस्पर बिंद P पर प्रतिच्छेद करते हैंक्या ΔPBC ~ ΔPDE है? क्यों?
दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात `3/5` है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनपात `6/5` है? क्यों?
ΔXYZ मे XY = 4 सेमी, YZ = 6 सेमी, XZ = 5 सेमी, यदि ΔXYZ ~ ΔPQR तथा PQ = 8 सेमी हो तो ΔPQR की शेष भुजाओं की लंबाई ज्ञात कीजिए।
