Advertisements
Advertisements
प्रश्न
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।(याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
उत्तर १

दी गई आकृति पर विचार करें जिसमें l एक रेखा है जो रेखाखंड AB के मध्य बिंदु P से होकर AC से Q पर मिलती है, इस प्रकार PQ || BC
मूल आनुपातिकता सिद्धांत का उपयोग करके, हम प्राप्त करते हैं
`(AQ)/(QC) = (AP)/(PB)`
`(AQ)/(QC) = 1/1` (P, AB का मध्य बिंदु है ∴ AP = PB)
⇒ AQ = QC
या, Q, AC का मध्य बिंदु है।
उत्तर २
PQ मध्य-बिंदु P और Q को मिलाने वाली रेखा है। वह AB और AC को इस प्रकार प्रतिछेद करती है की
PQ || BC
AP = PB ....(i)
आधारभूत समानुपातिकता प्रमेय से,
`"AP"/"PB" = "AQ"/"QC"` ....(ii)
अतः (i) एवं (ii) से
`"AP"/"PB" = "AQ"/"QC" = 1`
AQ = QC, Q मध्य-बिंदु है।
APPEARS IN
संबंधित प्रश्न
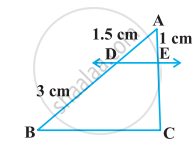
आकृति में, DE || BC है। EC ज्ञात कीजिए:
किसी ∆PQR की भुजाओं PQ और PR पर क्रमशः बिंदु E और F स्थित हैं। निम्नलिखित स्थिति के लिए, बताइए कि क्या EF || QR है:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
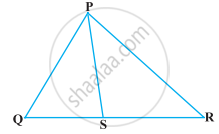
आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि `"QS"/"SR" = "PQ"/"PR"` है।
यदि ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm और BC = 15 cm है, तो PR बराबर ______ है।
ΔDEF ~ ΔRPQ दिया है। क्या कहना सत्य है कि ∠D = ∠R और ∠F = ∠P? क्यों?
क्या निम्नलिखित कथन सत्य है? क्यों?
“दो चतर्भज समरूप होते हैं. यदि उनके संगत कोण बराबर हों”
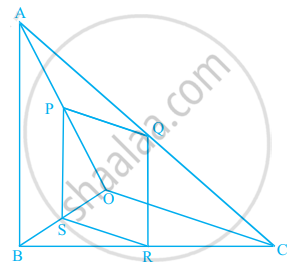
आकृति में, यदि PQRS एक समांतर चतुर्भुज है तथा AB || PS है, तो सिद्ध कीजिए कि OC || SR है।
ΔXYZ मे XY = 4 सेमी, YZ = 6 सेमी, XZ = 5 सेमी, यदि ΔXYZ ~ ΔPQR तथा PQ = 8 सेमी हो तो ΔPQR की शेष भुजाओं की लंबाई ज्ञात कीजिए।
समरूप त्रिभुजों की जोड़ी की कच्ची आकृति बनाइए । उन्हें नाम दें । उनके सर्वांगसम कोण समान चिह्नों से दर्शाएँ । त्रिभुजों की संगत भुजाओं की लंबाइयाँ समानुपात में हों ऐसी संख्याएँ दर्शाइए ।
