Advertisements
Advertisements
प्रश्न
आधारभूत समानुपातिकता प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं)।
उत्तर
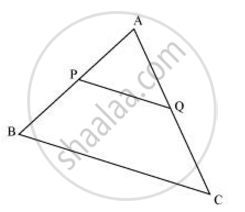
दी गई आकृति पर विचार करें जिसमें PQ क्रमशः रेखा AB और AC के मध्य-बिंदु P और Q को मिलाने वाला एक रेखाखंड है।
अर्थात, AP = PB और AQ = QC
यह देखा जा सकता है कि
`("AP")/("PB") = 1/1`
और `("AQ")/("QC") = 1/1`
∴ `("AP")/("PB") = ("AQ")/("QC")`
अतः, मूल समानुपातिकता प्रमेय का उपयोग करके, हम प्राप्त करते हैं
PQ || BC
APPEARS IN
संबंधित प्रश्न
आकृति में यदि LM || CB और LN || CD हो तो सिद्ध कीजिए कि `"AM"/"AB" = "AN"/"AD"` है।

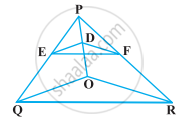
आकृति में DE || OQ और DF || OR है। दर्शाइए कि EF || QR है।
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि `("AO")/("BO") = ("CO")/("DO")` है। दर्शाइए कि ABCD एक समलंब है।
यदि ∆ABC ~ ∆QRP, `(ar(ABC))/(ar(PQR)) = 9/4`, AB = 18 cm और BC = 15 cm है, तो PR बराबर ______ है।
ΔDEF ~ ΔRPQ दिया है। क्या कहना सत्य है कि ∠D = ∠R और ∠F = ∠P? क्यों?
किसी त्रिभुज PQR की भुजाओं PQ और PR पर क्रमश : बिंद A और B इस प्रकार स्थित हैं कि PQ = 12.5 cm, PA = 5 cm, BR = 6 cm और PB = 4 cm हैं। क्या AB || QR है? अपने उत्तर के लिए कारण दीजिए।
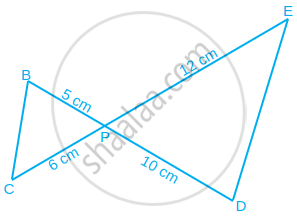
आकृति में BD और CE परस्पर बिंद P पर प्रतिच्छेद करते हैंक्या ΔPBC ~ ΔPDE है? क्यों?
क्या निम्नलिखित कथन सत्य है? क्यों?
“दो चतर्भज समरूप होते हैं. यदि उनके संगत कोण बराबर हों”
दो समरूप त्रिभुजों के संगत शीर्षलंबों का अनुपात `3/5` है। क्या यह कहना सही है कि इन त्रिभुजों के क्षेत्रफलों का अनपात `6/5` है? क्यों?
ΔXYZ मे XY = 4 सेमी, YZ = 6 सेमी, XZ = 5 सेमी, यदि ΔXYZ ~ ΔPQR तथा PQ = 8 सेमी हो तो ΔPQR की शेष भुजाओं की लंबाई ज्ञात कीजिए।
